SLR: Simulation-based inference

Hypothesis tests for the slope

Prof. Maria Tackett

Sep 14, 2022

Announcements

  • HW 01

    • Released later today (will get email when HW is available)

    • due Wed, Sep 21 at 11:59pm

  • Statistics experience - due Fri, Dec 09 at 11:59pm

  • See Week 03 for this week’s activities.

Topics

  • Evaluate a claim about the slope using hypothesis testing

  • Define mathematical models to conduct inference for slope

Computational setup

# load packages
library(tidyverse)   # for data wrangling and visualization
library(tidymodels)  # for modeling
library(usdata)      # for the county_2019 dataset
library(openintro)   # for Duke Forest dataset
library(scales)      # for pretty axis labels
library(glue)        # for constructing character strings
library(knitr)       # for neatly formatted tables
library(kableExtra)  # also for neatly formatted tablesf


# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_bw(base_size = 16))

Recap of last lecture

Data: Duke Forest houses

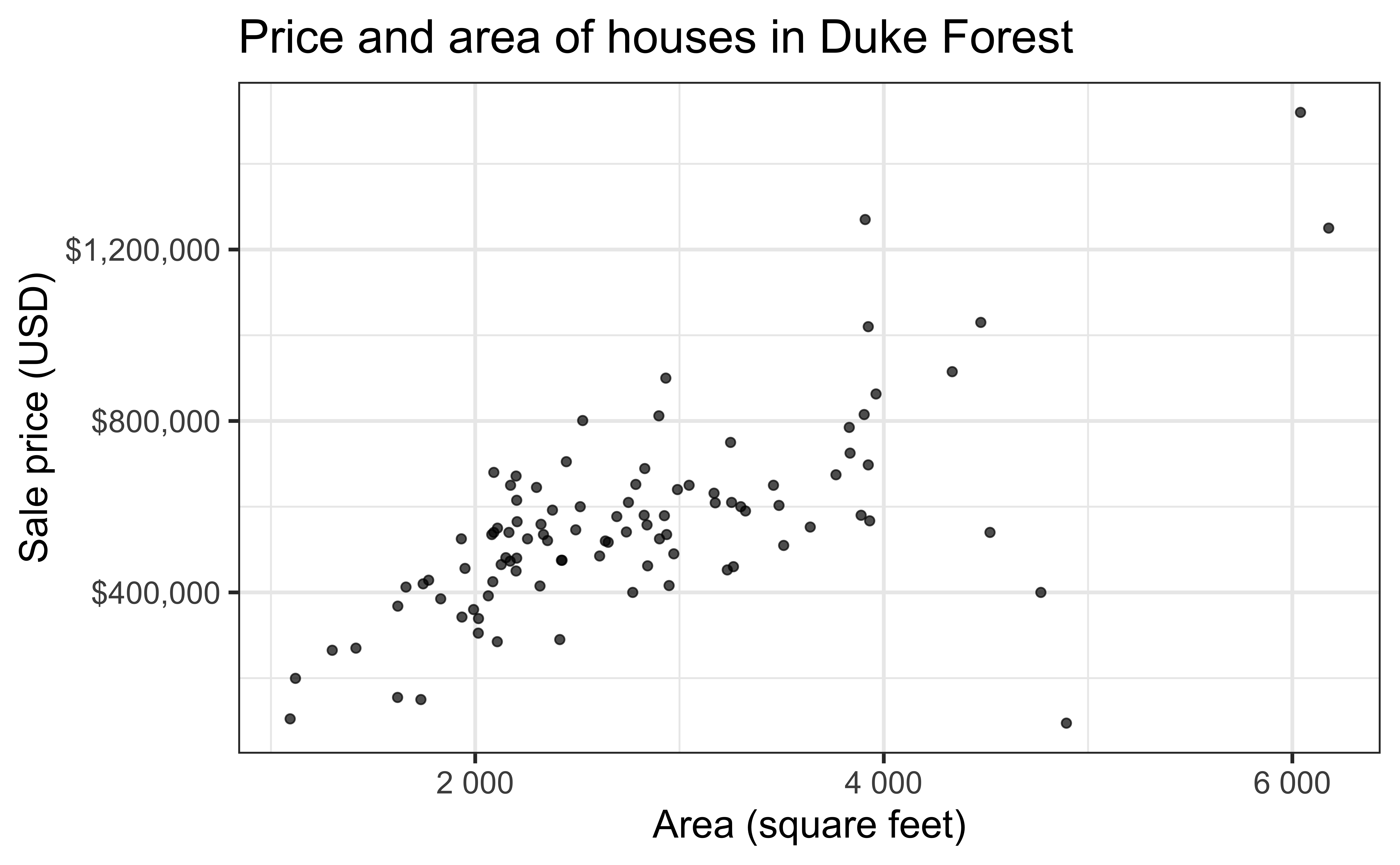
The regression model

df_fit <- linear_reg() |>
  set_engine("lm") |>
  fit(price ~ area, data = duke_forest)

tidy(df_fit) |>
  kable(digits = 2)
term estimate std.error statistic p.value
(Intercept) 116652.33 53302.46 2.19 0.03
area 159.48 18.17 8.78 0.00
  • Intercept: Duke Forest houses that are 0 square feet are expected to sell, on average, for $116,652.
  • Slope: For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $159.

Inference for simple linear regression

  • Calculate a confidence interval for the slope, β1

  • Conduct a hypothesis test for the slope, β1

Sampling is natural

Illustration of a bowl of soup
  • When you taste a spoonful of soup and decide the spoonful you tasted isn’t salty enough, that’s exploratory analysis
  • If you generalize and conclude that your entire soup needs salt, that’s an inference
  • For your inference to be valid, the spoonful you tasted (the sample) needs to be representative of the entire pot (the population)

Confidence interval via bootstrapping

  • Bootstrap new samples from the original sample
  • Fit models to each of the samples and estimate the slope
  • Use features of the distribution of the bootstrapped slopes to construct a confidence interval

Bootstrapping pipeline I

set.seed(210)

duke_forest |>
  specify(price ~ area)set.seed(210)

duke_forest |>
  specify(price ~ area)set.seed(210)

duke_forest |>
  specify(price ~ area)set.seed(210)

duke_forest |>
  specify(price ~ area)
Response: price (numeric)
Explanatory: area (numeric)
# A tibble: 98 × 2
     price  area
     <dbl> <dbl>
 1 1520000  6040
 2 1030000  4475
 3  420000  1745
 4  680000  2091
 5  428500  1772
 6  456000  1950
 7 1270000  3909
 8  557450  2841
 9  697500  3924
10  650000  2173
# … with 88 more rows

Bootstrapping pipeline II

set.seed(210)

duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap")set.seed(210)

duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap")
Response: price (numeric)
Explanatory: area (numeric)
# A tibble: 98,000 × 3
# Groups:   replicate [1,000]
   replicate   price  area
       <int>   <dbl> <dbl>
 1         1  290000  2414
 2         1  285000  2108
 3         1  265000  1300
 4         1  416000  2949
 5         1  541000  2740
 6         1  525000  2256
 7         1 1270000  3909
 8         1  265000  1300
 9         1  815000  3904
10         1  535000  2937
# … with 97,990 more rows

Bootstrapping pipeline III

set.seed(210)

duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()set.seed(210)

duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()
# A tibble: 2,000 × 3
# Groups:   replicate [1,000]
   replicate term      estimate
       <int> <chr>        <dbl>
 1         1 intercept   80699.
 2         1 area          168.
 3         2 intercept  -18821.
 4         2 area          205.
 5         3 intercept  234297.
 6         3 area          117.
 7         4 intercept  134481.
 8         4 area          150.
 9         5 intercept   23861.
10         5 area          190.
# … with 1,990 more rows

Bootstrapping pipeline IV

set.seed(210)

boot_dist <- duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()set.seed(210)

boot_dist <- duke_forest |>
  specify(price ~ area) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()

Visualize the bootstrap distribution

boot_dist |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram(binwidth = 10)boot_dist |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram(binwidth = 10)

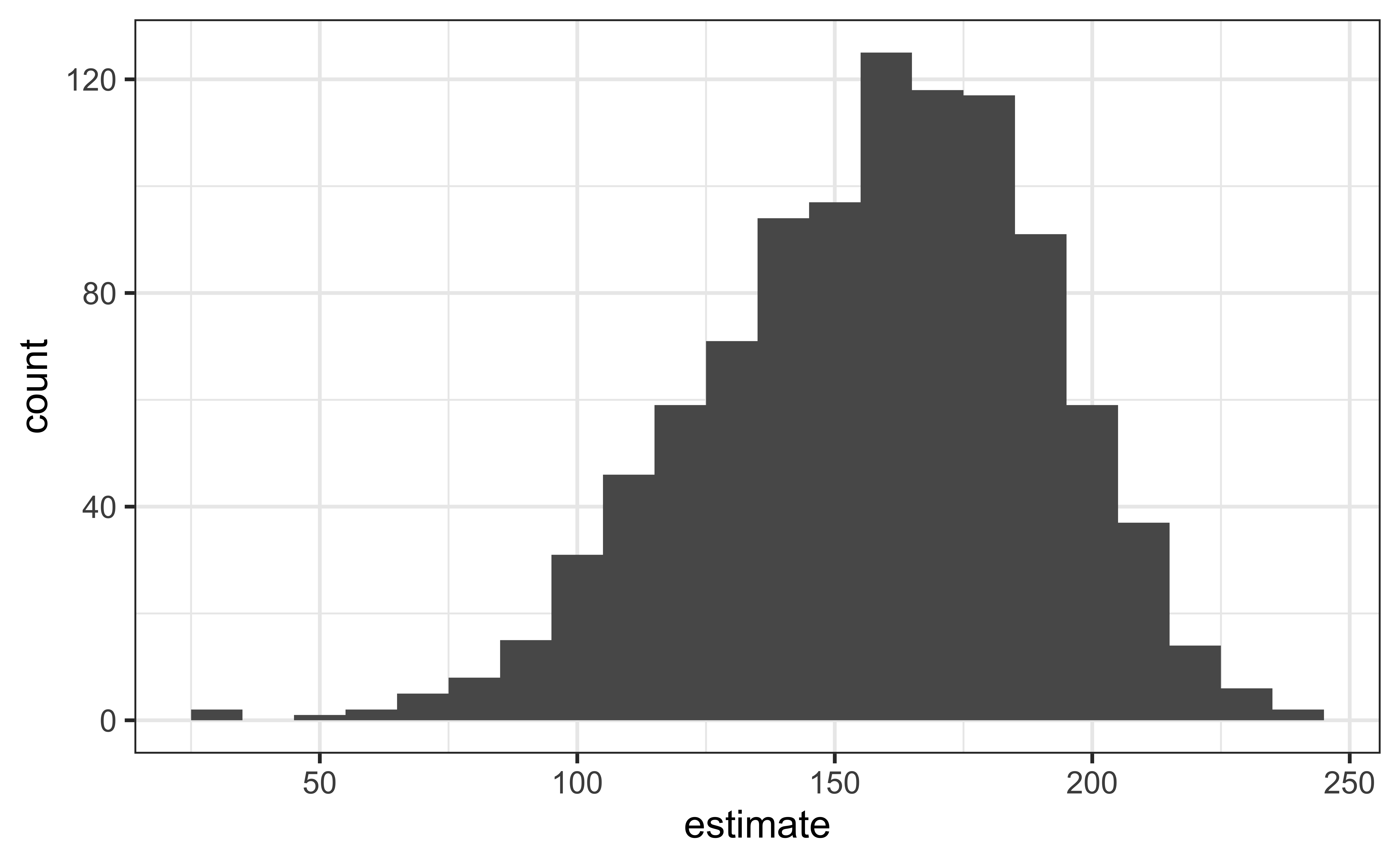
Compute the CI

But first…

obs_fit <- duke_forest |>
  specify(price ~ area) |>
  fit()

obs_fit
# A tibble: 2 × 2
  term      estimate
  <chr>        <dbl>
1 intercept  116652.
2 area          159.

Compute 95% confidence interval

boot_dist |>
  get_confidence_interval(
    level = 0.95,
    type = "percentile",
    point_estimate = obs_fit
  )boot_dist |>
  get_confidence_interval(
    level = 0.95,
    type = "percentile",
    point_estimate = obs_fit
  )
# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 area          91.7     211.
2 intercept -18290.   287711.

Hypothesis test for the slope

Research question and hypotheses

  • “Do the data provide sufficient evidence that β1 (the true slope for the population) is different from 0?”

  • Null hypothesis: there is no linear relationship between area and price

    H0:β1=0

    Alternative hypothesis: there is a linear relationship between area and price

    HA:β1≠0

Hypothesis testing as a court trial

  • Null hypothesis, H0: Defendant is innocent
  • Alternative hypothesis, HA: Defendant is guilty
  • Present the evidence: Collect data
  • Judge the evidence: “Could these data plausibly have happened by chance if the null hypothesis were true?”

    • Yes: Fail to reject H0

    • No: Reject H0

Hypothesis testing framework

  • Start with a null hypothesis, H0 that represents the status quo
  • Set an alternative hypothesis, HA that represents the research question, i.e. what we’re testing for
  • Conduct a hypothesis test under the assumption that the null hypothesis is true and calculate a p-value (probability of observed or more extreme outcome given that the null hypothesis is true)
    • if the test results suggest that the data do not provide convincing evidence for the alternative hypothesis, stick with the null hypothesis
    • if they do, then reject the null hypothesis in favor of the alternative

Quantify the variability of the slope

for testing

  • Two approaches:
    1. Via simulation
    2. Via mathematical models
  • Randomization to quantify the variability of the slope for the purpose of testing, under the assumption that the null hypothesis is true:
    • Simulate new samples from the original sample via permutation
    • Fit models to each of the samples and estimate the slope
    • Use features of the distribution of the permuted slopes to conduct a hypothesis test

Permutation, described

  • Set the null hypothesis to be true, and measure the natural variability in the data due to sampling but not due to variables being correlated by permuting
    • Permute one variable to eliminate any existing relationship between the variables
  • Each price value is randomly assigned to area of a given house, i.e. area and price are no longer matched for a given house
# A tibble: 98 × 3
   price_Observed price_Permuted  area
            <dbl>          <dbl> <dbl>
 1        1520000         342500  6040
 2        1030000         750000  4475
 3         420000         645000  1745
 4         680000         697500  2091
 5         428500         428500  1772
 6         456000         481000  1950
 7        1270000         610000  3909
 8         557450         680000  2841
 9         697500         485000  3924
10         650000         105000  2173
# … with 88 more rows

Permutation, visualized

  • Each of the observed values for area (and for price) exist in both the observed data plot as well as the permuted price plot
  • The permutation removes the linear relationship between area and price

Permutation, repeated

Repeated permutations allow for quantifying the variability in the slope under the condition that there is no linear relationship (i.e., that the null hypothesis is true)

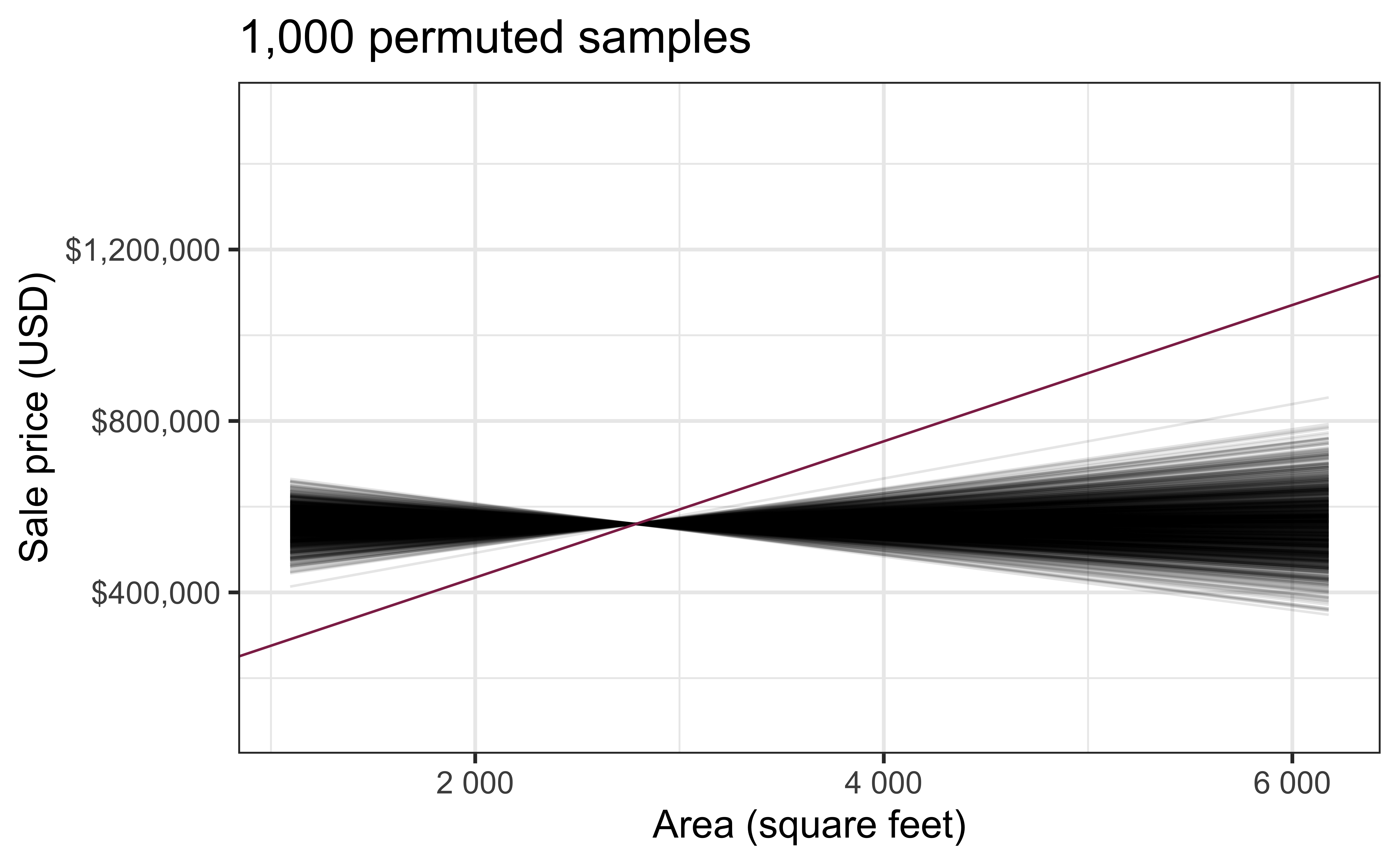
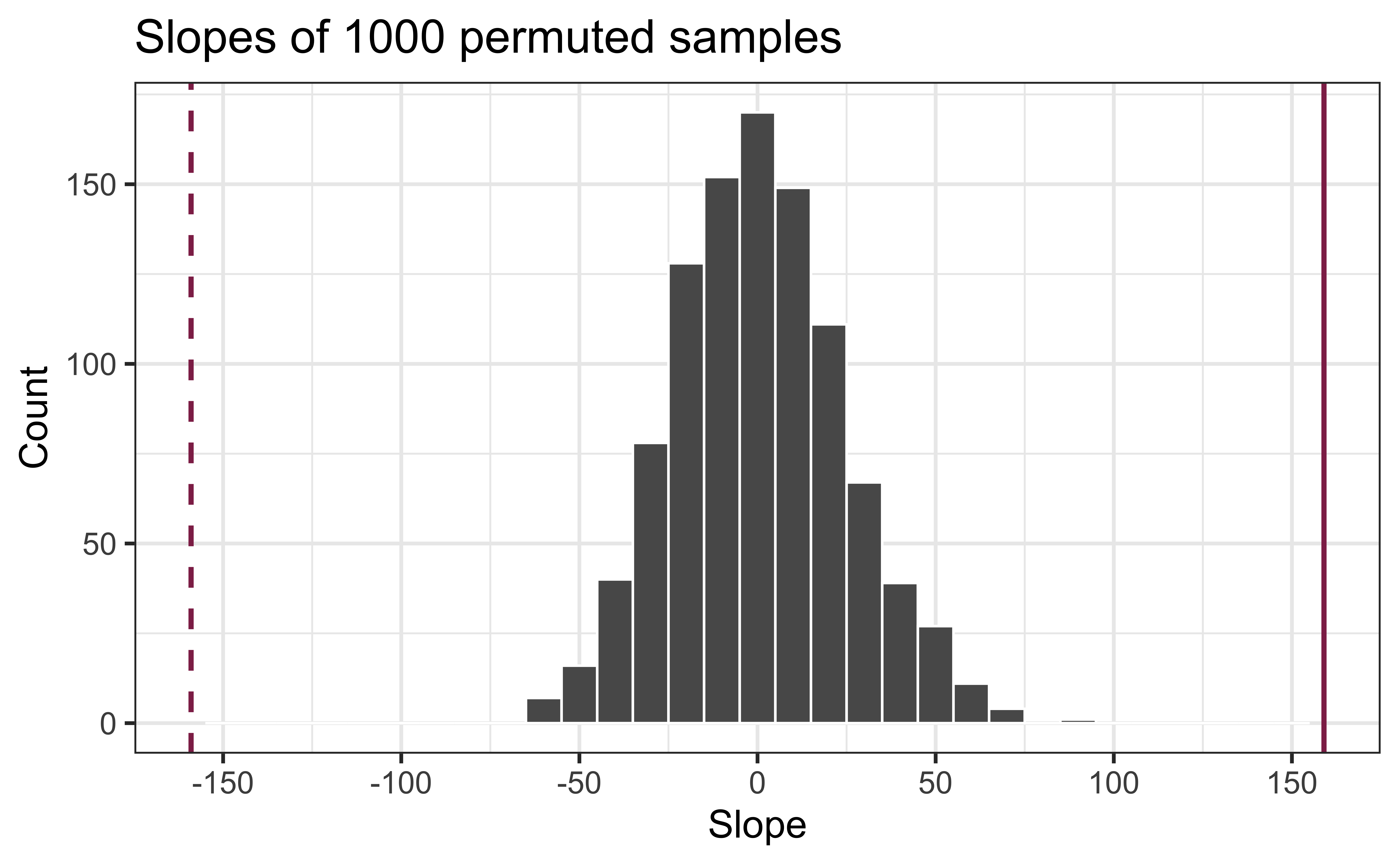
Concluding the hypothesis test

Is the observed slope of ^β1=159 (or an even more extreme slope) a likely outcome under the null hypothesis that β=0? What does this mean for our original question: “Do the data provide sufficient evidence that β1 (the true slope for the population) is different from 0?”

Application exercise

📋 AE 04: Simulation-based hypothesis testing

Permutation pipeline I

set.seed(1125)

duke_forest |>
  specify(price ~ area)set.seed(1125)

duke_forest |>
  specify(price ~ area)set.seed(1125)

duke_forest |>
  specify(price ~ area)set.seed(1125)

duke_forest |>
  specify(price ~ area)
Response: price (numeric)
Explanatory: area (numeric)
# A tibble: 98 × 2
     price  area
     <dbl> <dbl>
 1 1520000  6040
 2 1030000  4475
 3  420000  1745
 4  680000  2091
 5  428500  1772
 6  456000  1950
 7 1270000  3909
 8  557450  2841
 9  697500  3924
10  650000  2173
# … with 88 more rows

Permutation pipeline II

set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence")set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence")
Response: price (numeric)
Explanatory: area (numeric)
Null Hypothesis: independence
# A tibble: 98 × 2
     price  area
     <dbl> <dbl>
 1 1520000  6040
 2 1030000  4475
 3  420000  1745
 4  680000  2091
 5  428500  1772
 6  456000  1950
 7 1270000  3909
 8  557450  2841
 9  697500  3924
10  650000  2173
# … with 88 more rows

Permutation pipeline III

set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute")set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute")
Response: price (numeric)
Explanatory: area (numeric)
Null Hypothesis: independence
# A tibble: 98,000 × 3
# Groups:   replicate [1,000]
     price  area replicate
     <dbl> <dbl>     <int>
 1  465000  6040         1
 2  481000  4475         1
 3 1020000  1745         1
 4  520000  2091         1
 5  592000  1772         1
 6  650000  1950         1
 7  473000  3909         1
 8  705000  2841         1
 9  785000  3924         1
10  671500  2173         1
# … with 97,990 more rows

Permutation pipeline IV

set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()set.seed(1125)

duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()
# A tibble: 2,000 × 3
# Groups:   replicate [1,000]
   replicate term       estimate
       <int> <chr>         <dbl>
 1         1 intercept 553355.  
 2         1 area           2.35
 3         2 intercept 635824.  
 4         2 area         -27.3 
 5         3 intercept 536072.  
 6         3 area           8.57
 7         4 intercept 598649.  
 8         4 area         -13.9 
 9         5 intercept 556202.  
10         5 area           1.33
# … with 1,990 more rows

Permutation pipeline V

set.seed(1125)

null_dist <- duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()set.seed(1125)

null_dist <- duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()

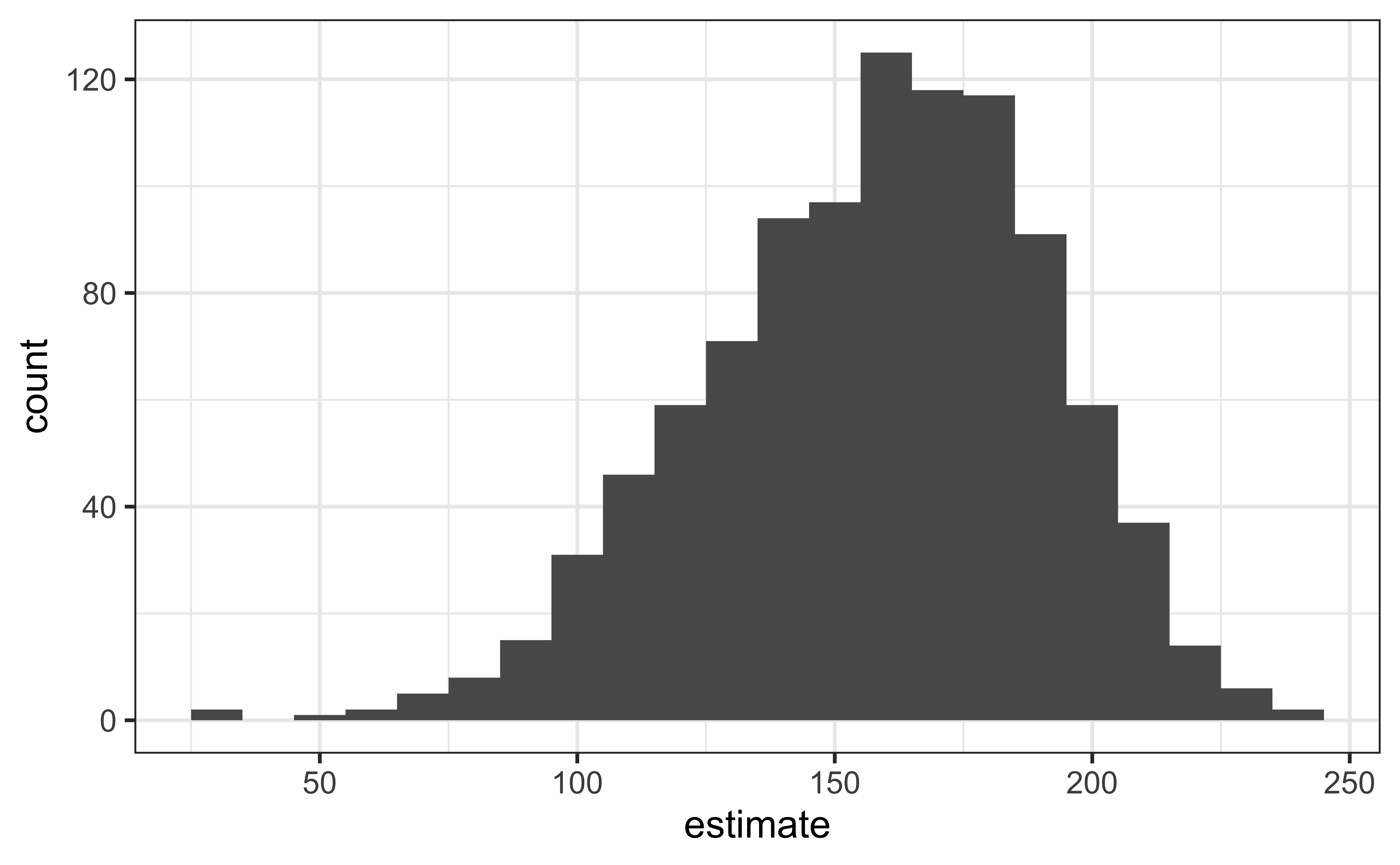
Visualize the null distribution

null_dist |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram(binwidth = 10, color = "white")null_dist |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram(binwidth = 10, color = "white")

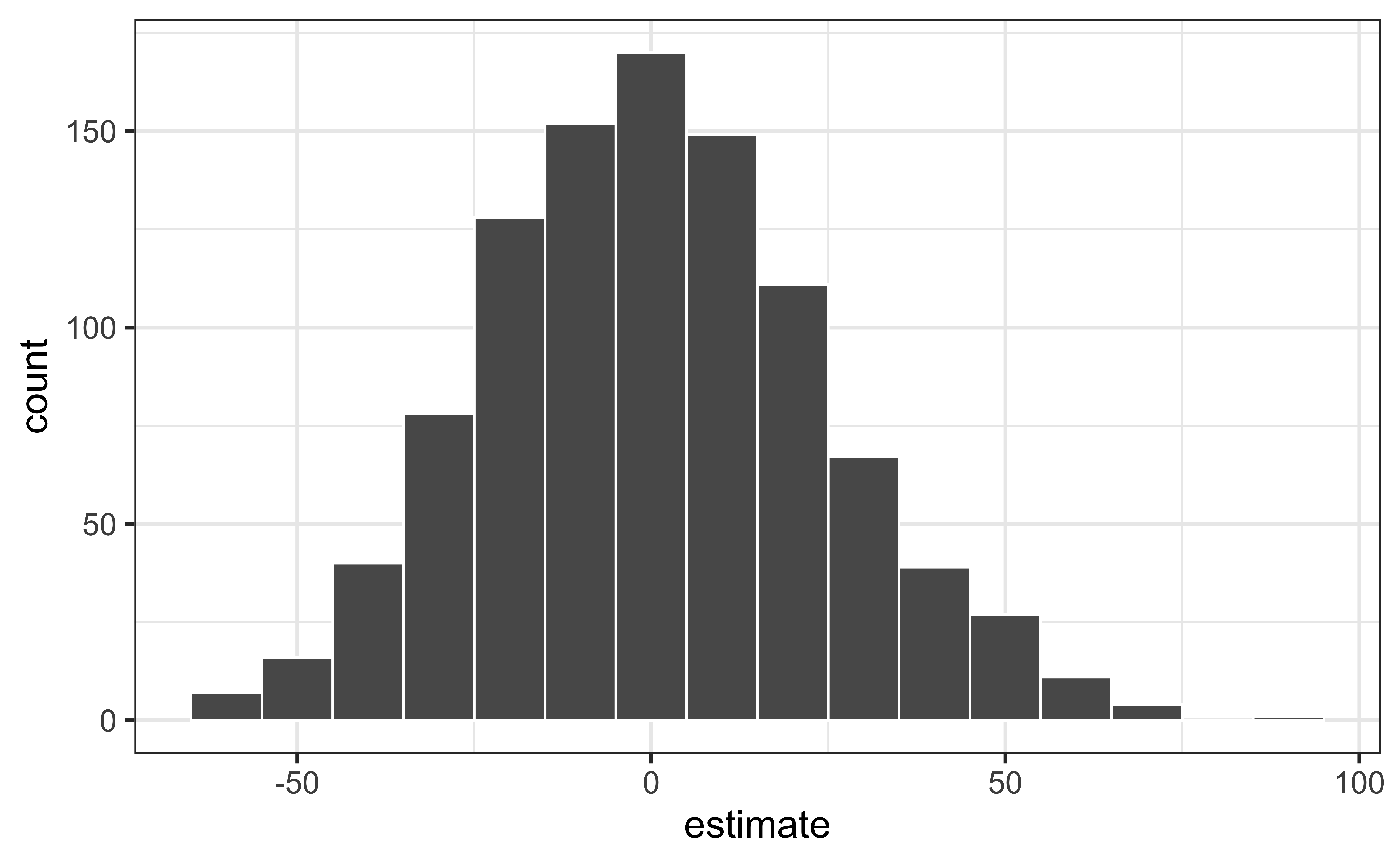
Reason around the p-value

In a world where the there is no relationship between the area of a Duke Forest house and in its price (β1=0), what is the probability that we observe a sample of 98 houses where the slope fo the model predicting price from area is 159 or even more extreme?

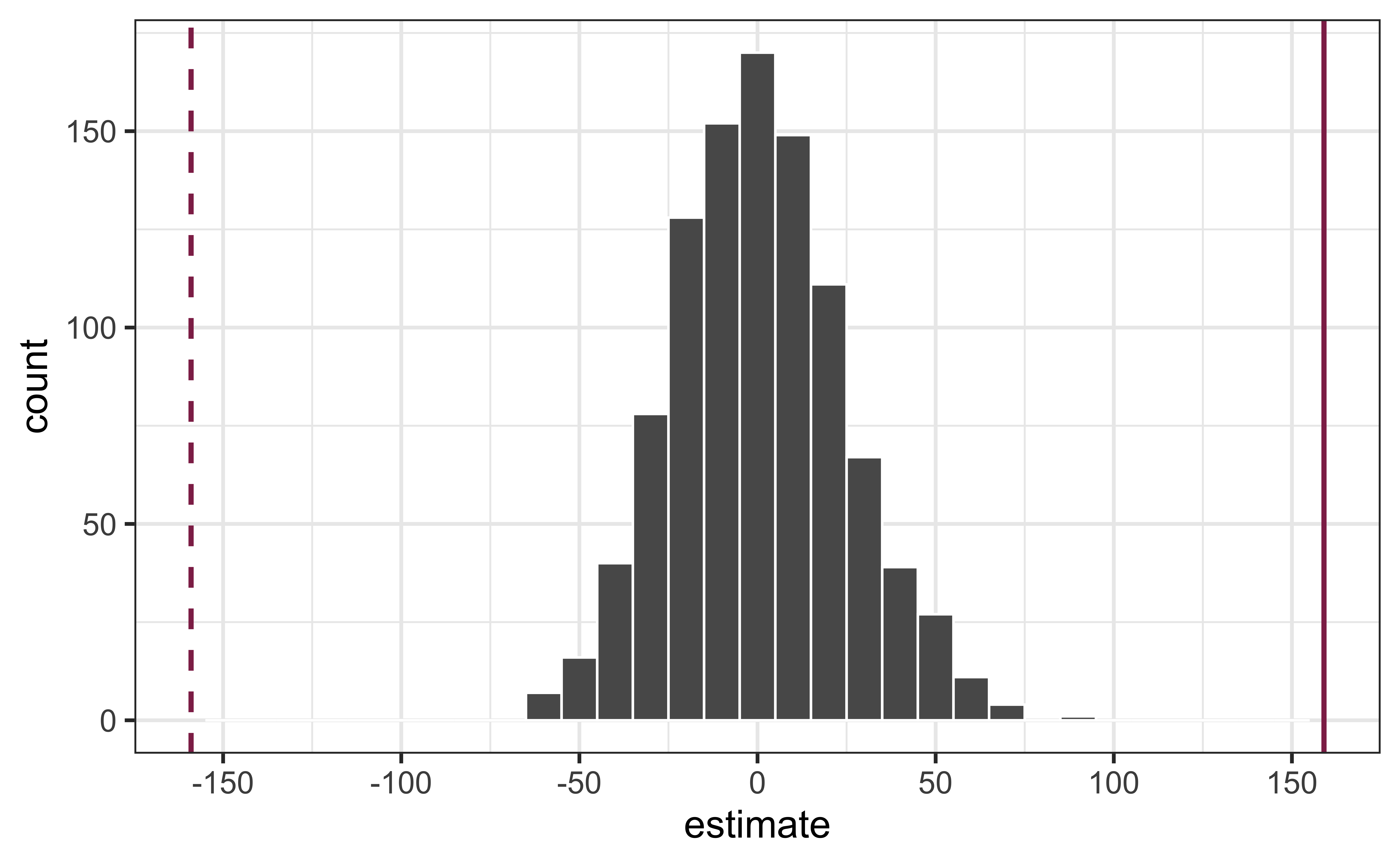
Compute the p-value

What does this warning mean?

get_p_value(
  null_dist,
  obs_stat = obs_fit,
  direction = "two-sided"
)
Warning: Please be cautious in reporting a p-value of 0. This result is an
approximation based on the number of `reps` chosen in the `generate()` step. See
`?get_p_value()` for more information.

Warning: Please be cautious in reporting a p-value of 0. This result is an
approximation based on the number of `reps` chosen in the `generate()` step. See
`?get_p_value()` for more information.
# A tibble: 2 × 2
  term      p_value
  <chr>       <dbl>
1 area            0
2 intercept       0

Mathematical models for inference

The regression model, revisited

df_fit <- linear_reg() |>
  set_engine("lm") |>
  fit(price ~ area, data = duke_forest)

tidy(df_fit) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 116652.325 53302.463 2.188 0.031
area 159.483 18.171 8.777 0.000

Inference, revisited

  • Earlier we computed a confidence interval and conducted a hypothesis test via simulation:
    • CI: Bootstrap the observed sample to simulate the distribution of the slope
    • HT: Permute the observed sample to simulate the distribution of the slope under the assumption that the null hypothesis is true
  • Now we’ll do these based on theoretical results, i.e., by using the Central Limit Theorem to define the distribution of the slope and use features (shape, center, spread) of this distribution to compute bounds of the confidence interval and the p-value for the hypothesis test

Mathematical representation of the model

Y=Model+Error=f(X)+ϵ=μY|X+ϵ=β0+β1X+ϵ

where the errors are independent and normally distributed:

  • independent: Knowing the error term for one observation doesn’t tell you anything about the error term for another observation
  • normally distributed: ϵ∼N(0,σ2ϵ)

Mathematical representation, visualized

Y|X∼N(β0+β1X,σ2ϵ)

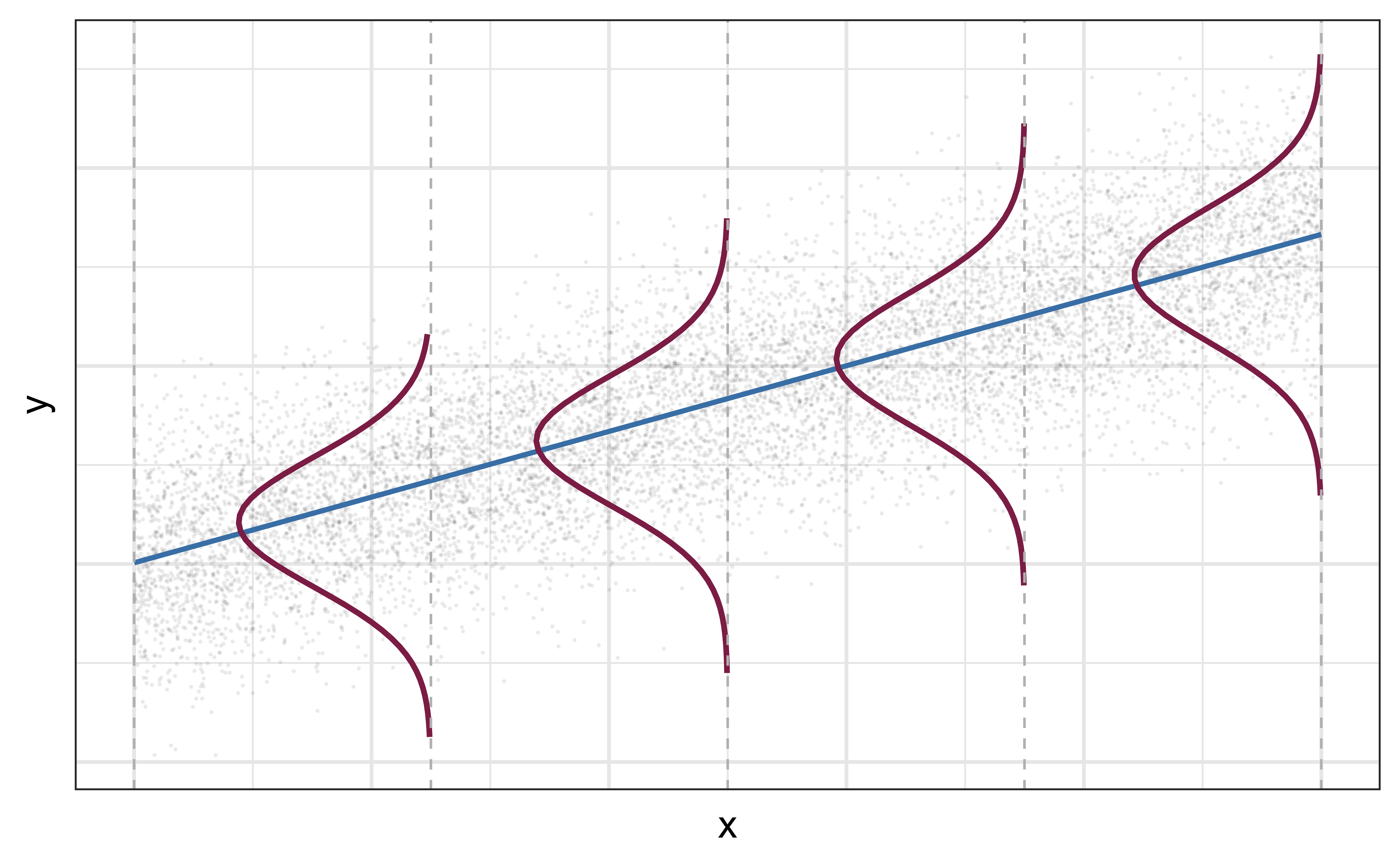
  • Mean: β0+β1X, the predicted value based on the regression model
  • Variance: σ2ϵ, constant across the range of X
    • How do we estimate σ2ϵ?

Regression standard error

Once we fit the model, we can use the residuals to estimate the regression standard error (the spread of the distribution of the response, for a given value of the predictor variable):

ˆσϵ=√n∑i=1(yi−ˆyi)2n−2=√n∑i=1e2in−2

  1. Why divide by n−2?
  2. Why do we care about the value of the regression standard error?

Standard error of ˆβ1

SEˆβ1=ˆσϵ√1(n−1)s2X

or…

term estimate std.error statistic p.value
(Intercept) 116652.33 53302.46 2.19 0.03
area 159.48 18.17 8.78 0.00

🔗 Week 03

1 / 43
SLR: Simulation-based inference Hypothesis tests for the slope Prof. Maria Tackett Sep 14, 2022

  1. Slides

  2. Tools

  3. Close
  • SLR: Simulation-based inference
  • Announcements
  • Topics
  • Computational setup
  • Recap of last lecture
  • Data: Duke Forest houses
  • The regression model
  • Inference for simple linear regression
  • Sampling is natural
  • Confidence interval via bootstrapping
  • Bootstrapping pipeline I
  • Bootstrapping pipeline II
  • Bootstrapping pipeline III
  • Bootstrapping pipeline IV
  • Visualize the bootstrap distribution
  • Compute the CI
  • But first…
  • Compute 95% confidence interval
  • Hypothesis test for the slope
  • Research question and hypotheses
  • Hypothesis testing as a court trial
  • Hypothesis testing framework
  • Quantify the variability of the slope
  • Permutation, described
  • Permutation, visualized
  • Permutation, repeated
  • Concluding the hypothesis test
  • Application exercise
  • Permutation pipeline I
  • Permutation pipeline II
  • Permutation pipeline III
  • Permutation pipeline IV
  • Permutation pipeline V
  • Visualize the null distribution
  • Reason around the p-value
  • Compute the p-value
  • Mathematical models for inference
  • The regression model, revisited
  • Inference, revisited
  • Mathematical representation of the model
  • Mathematical representation, visualized
  • Regression standard error
  • Standard error of \(\hat{\beta}_1\)
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help