Fitting multilevel models

Prof. Maria Tackett

Nov 30, 2022

Announcements

  • Due dates

    • Statistics experience due Fri, Dec 09, 11:59pm
    • Project written report due Fri, Dec 09, 11:59pm
    • Team Feedback #2 due Tue, Dec 06, 11:59pm (check for email from Teammates)

  • Exam 02: Mon, Dec 05 (evening) - Thu, Dec 08, 12pm (noon)

    • Exam 02 review on Mon Dec 05

    • Click here for lecture recordings - available until Dec 05, 11:59pm

  • See Week 14 activities

Learning goals

  • Understand how multilevel model can be used to take correlation into account
  • Interpret fixed effects of multilevel model
  • Fit multilevel model in R

Data: Music performance anxiety

The data musicdata.csv come from the Sadler and Miller (2010) study of the emotional state of musicians before performances. The dataset contains information collected from 37 undergraduate music majors who completed the Positive Affect Negative Affect Schedule (PANAS), an instrument produces a measure of anxiety (negative affect) and a measure of happiness (positive affect). This analysis will focus on negative affect as a measure of performance anxiety.

Data: Music performance anxiety

The primary variables we’ll use are

  • na: negative affect score on PANAS (the response variable)
  • perform_type: type of performance (Solo, Large Ensemble, Small Ensemble)
    • Create variable large_ensemble: 1 if large ensemble performance, 0 otherwise
  • instrument: type of instrument (Voice, Orchestral, Piano)
    • Create variable orchestra: 1 if orchestral instrument, 0 otherwise

Look at data

id diary large_ensemble orchestra na
1 1 0 0 11
1 2 1 0 19
1 3 1 0 14
43 1 0 0 19
43 2 0 0 13
43 3 0 0 19

Draw the data structure, and add the Level One and Level Two observational units and variables.

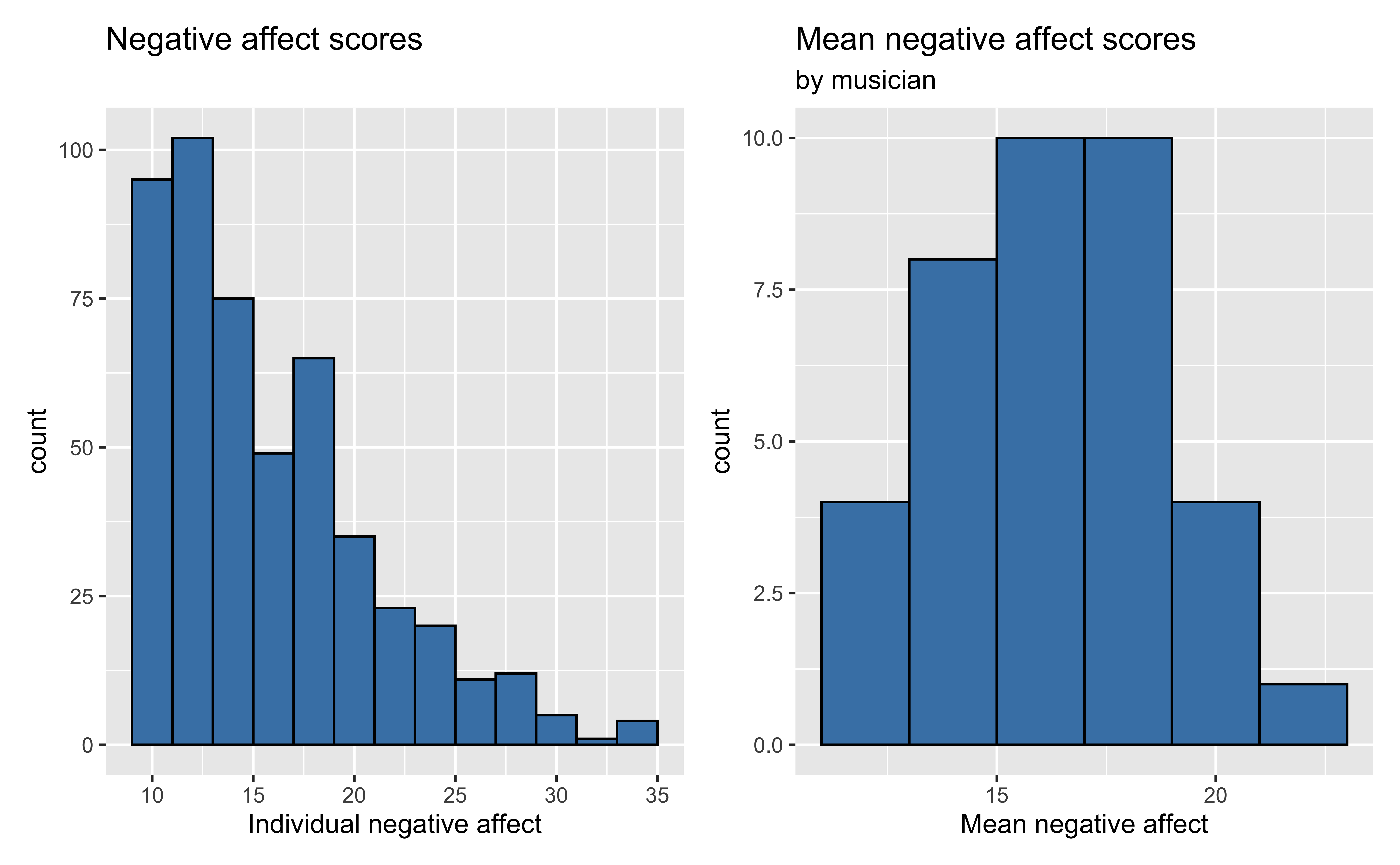
Unviariate EDA

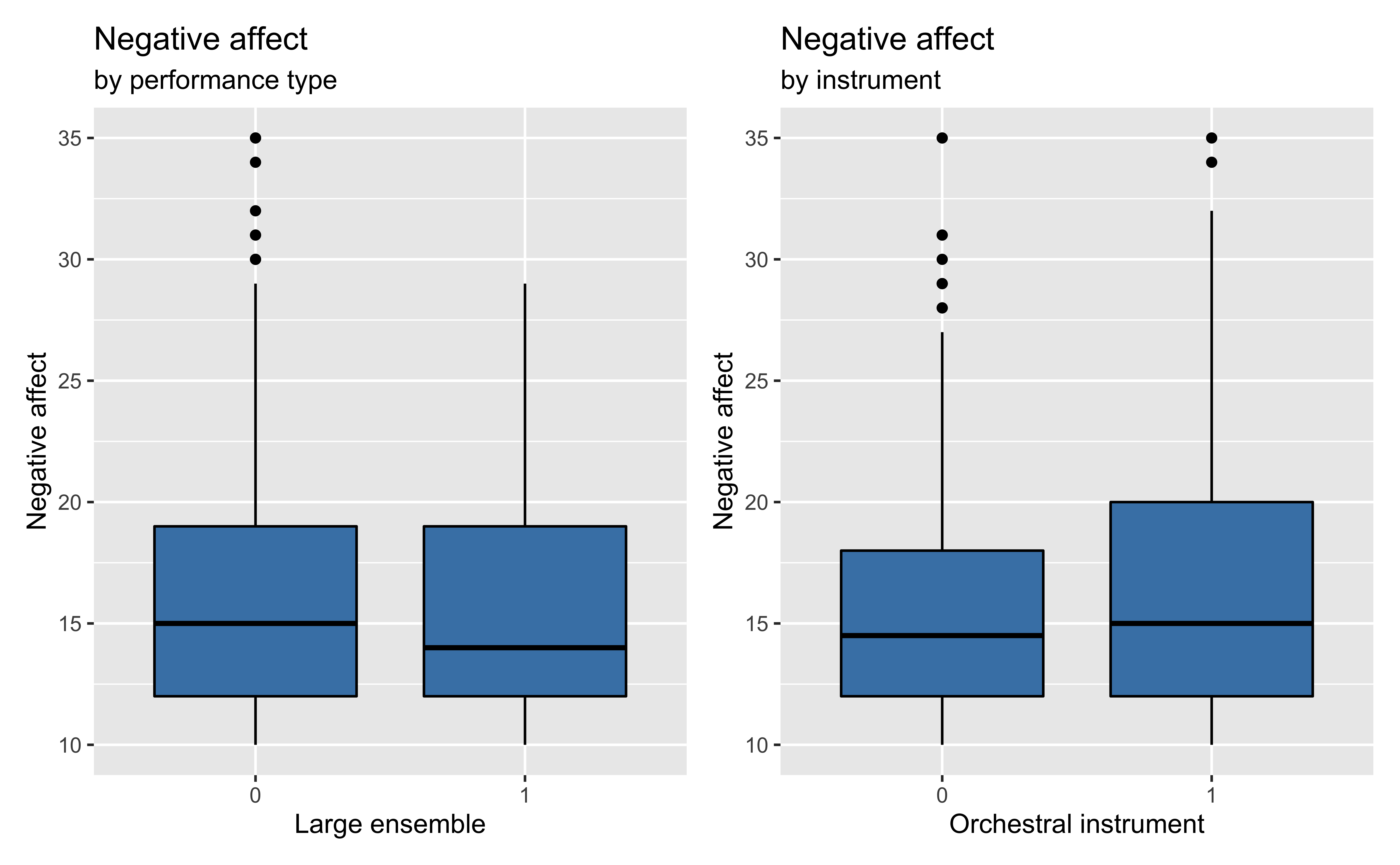
Bivariate EDA

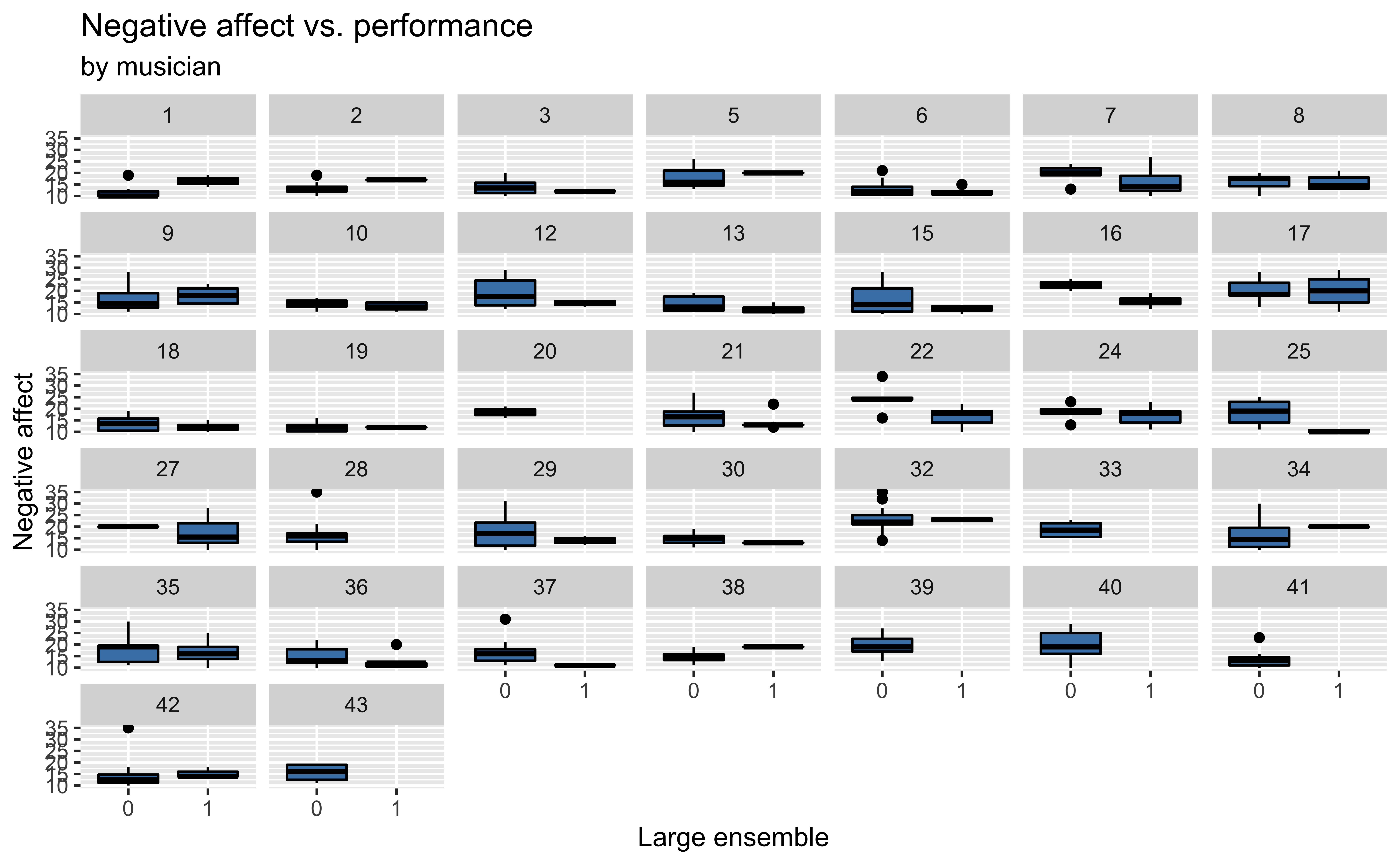
Bivariate EDA

Fitting the model

Questions we want to answer

The goal is to understand variability in performance anxiety (na) based on performance-level and musician-level characteristics. Specifically:

What is the association between performance type (large ensemble or not) and performance anxiety? Does the association differ based on instrument type (orchestral or not)?

Modeling workflow

We will fit the model in two parts:

1️⃣ Fit a separate model for each musician understand the association between performance type and anxiety (Level One models).

2️⃣ Then fit a system of models to predict the fitted coefficients in the Level One models based on instrument type (Level Two models).

  • How many Level One models will we fit?
  • How many Level Two models will we fit?

1️⃣ Level One model

We’ll start with the Level One model to understand the association between performance type and performance anxiety for the ith musician.

naij=ai+bi LargeEnsembleij+ϵi,ϵij∼N(0,σ2)

Why is it more meaningful to use performance type for the Level One model than instrument?

For now, estimate ai and bi using least-squares regression.

Level One model for one student

Below is partial data for observation #22

id diary large_ensemble orchestra na
22 1 0 1 24
22 2 1 1 21
22 3 1 1 14
22 13 1 1 12
22 14 1 1 19
22 15 0 1 25

Level One model for musician 22

id_22 <- music |>
  filter(id == 22)

linear_reg() |>
  set_engine("lm") |>
  fit(na ~ large_ensemble, data = id_22) |>
  tidy() |> kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 24.500 1.96 12.503 0.000
large_ensemble -7.833 2.53 -3.097 0.009

Application exercise

📋 AE 15: Introduction to Multilevel models

See Part 3: Level One Models to fit the Level One model for all 37 musicians.

Level One model summaries

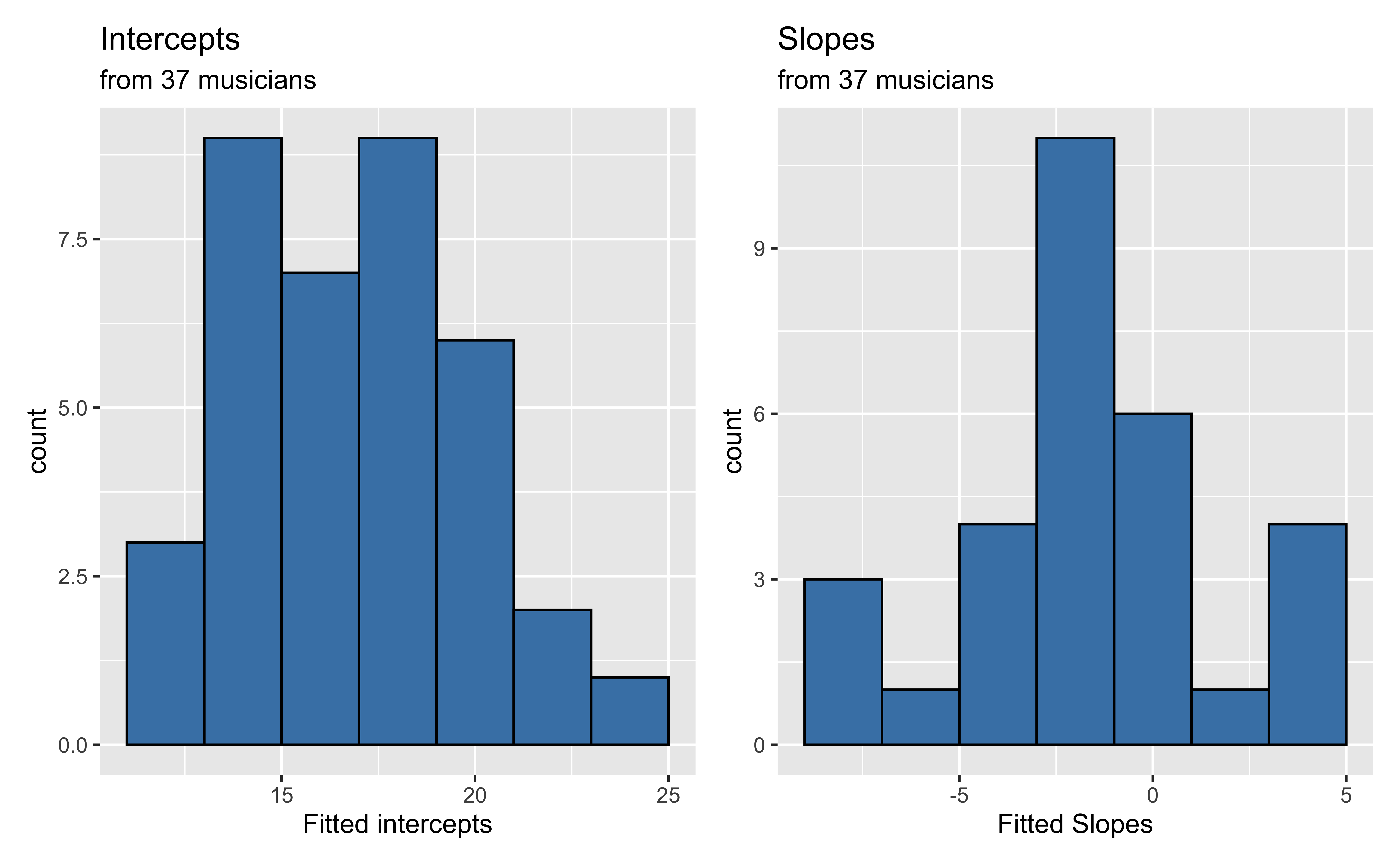
Recreated from BMLR Figure 8.9

Now let’s consider if there is an association between the estimated slopes, estimated intercepts, and the type of instrument.

Level Two Model

The slope and intercept for the ith musician can be modeled as

ai=α0+α1 Orchestrai+uibi=β0+β1 Orchestrai+vi

Note

The response variable in the Level Two models are not observed outcomes but the (fitted) slope and intercept from each musician

Application exercise

📋 AE 15: Introduction to Multilevel models

See Part 4: Level Two Models.

Estimated coefficients by instrument

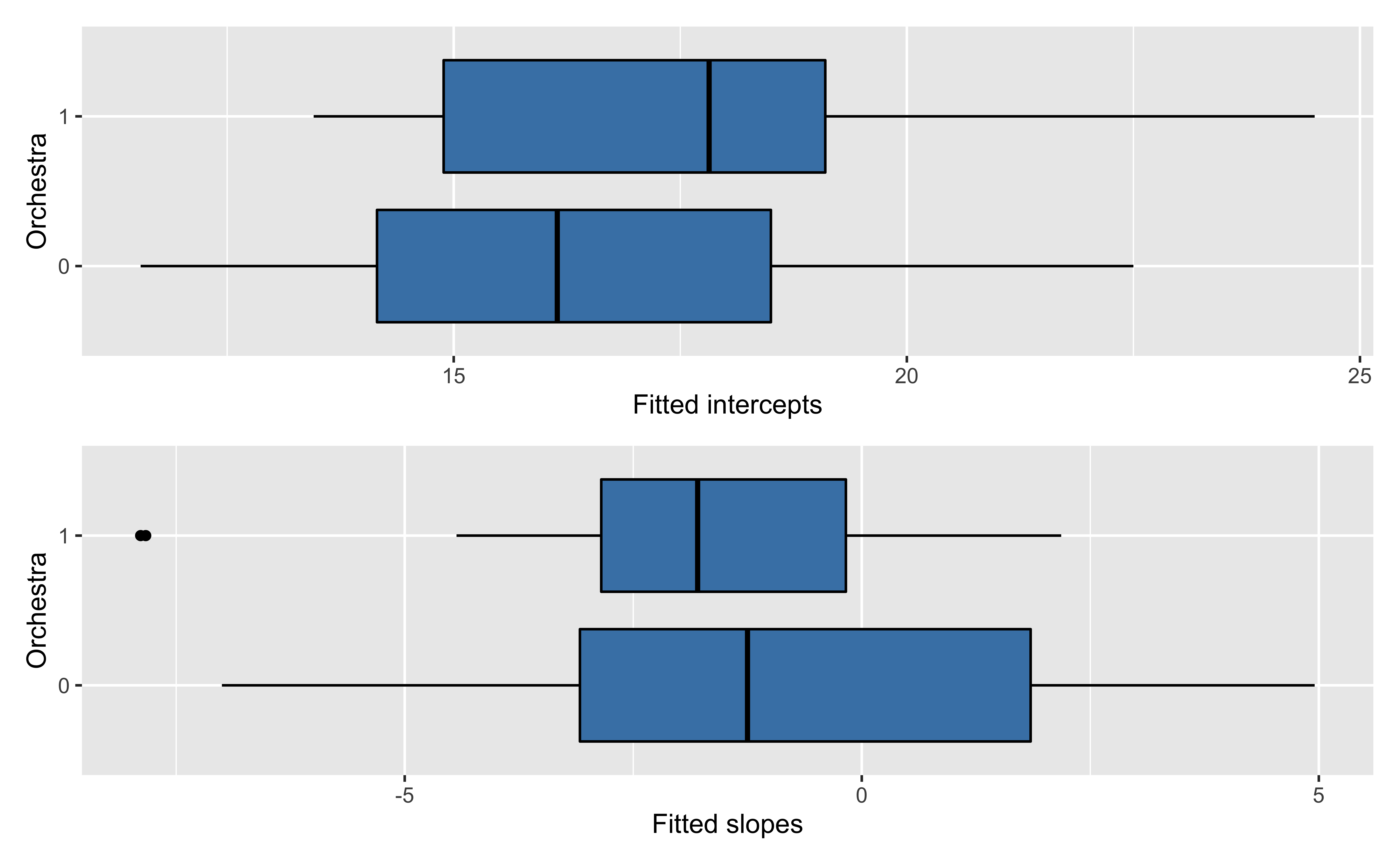
Level Two model

Model for intercepts

term estimate std.error statistic p.value
(Intercept) 16.283 0.671 24.249 0.000
orchestra 1.411 0.991 1.424 0.163

Model for slopes

term estimate std.error statistic p.value
(Intercept) -0.771 0.851 -0.906 0.373
orchestra -1.406 1.203 -1.168 0.253

Writing out the models

Level One

^naij=ˆai+ˆbi LargeEnsembleij

for each musician.

Level Two

ˆai=16.283+1.411 Orchestraiˆbi=−0.771−1.406 Orchestrai

Composite model

^nai=16.283+1.411 Orchestrai−0.771 LargeEnsembleij−1.406 Orchestra:LargeEnsembleij

  • What is the predicted average performance anxiety before solos and small ensemble performances for vocalists and keyboardists? For those who play orchestral instruments?

  • What is the predicted average performance anxiety before large ensemble performances for those who play orchestral instruments?

countdown(minutes = 3, seconds= 0)
03:00

Disadvantages to this approach

⚠️ Weighs each musician the same regardless of number of diary entries

⚠️ Drops subjects who have missing values for slope (7 individuals who didn’t play a large ensemble performance)

⚠️ Does not share strength effectively across individuals.

Application exercise

📋 AE 15: Introduction to Multilevel models

See Part 5: Distribution of R2 values.

Unified approach to two-level modeling

Framework

Let Yij be the performance anxiety for the ith musician before performance j.

Level One

Yij=ai+bi LargeEnsembleij+ϵij

Level Two

ai=α0+α1 Orchestrai+uibi=β0+β1 Orchestrai+vi

Coefficients are estimated using likelihood-based methods (instead of least squares) to address the previously mentioned disadvantages

Composite model

Plug in the equations for ai and bi to get the composite model Yij=(α0+α1 Orchestrai+β0 LargeEnsembleij+β1 Orchestrai:LargeEnsembleij)+(ui+vi LargeEnsembleij+ϵij)

  • The fixed effects to estimate are α0,α1,β0,β1
  • The error terms are ui,vi,ϵij
    • We will estimate variability in the error terms σu,σv,σϵ

Note

We no longer need to estimate ai and bi directly as we did earlier. They conceptually connect the Level One and Level Two models.

Error terms

  • We generally assume that the error terms are normally distributed, e.g. error associated with each performance of a given musician is ϵij∼N(0,σ2)

  • For the Level Two models, the errors are

    • ui: deviation of musician i from the mean performance anxiety before solos and small ensembles after accounting for the instrument
    • vi: deviance of musician i from the mean difference in performance anxiety between large ensembles and other performance types after accounting for instrument

  • We will also estimate ρuv to account for fact that ui (the intercepts) and vi (the slopes) are correlated for the ith musician

Slopes vs intercepts by musician

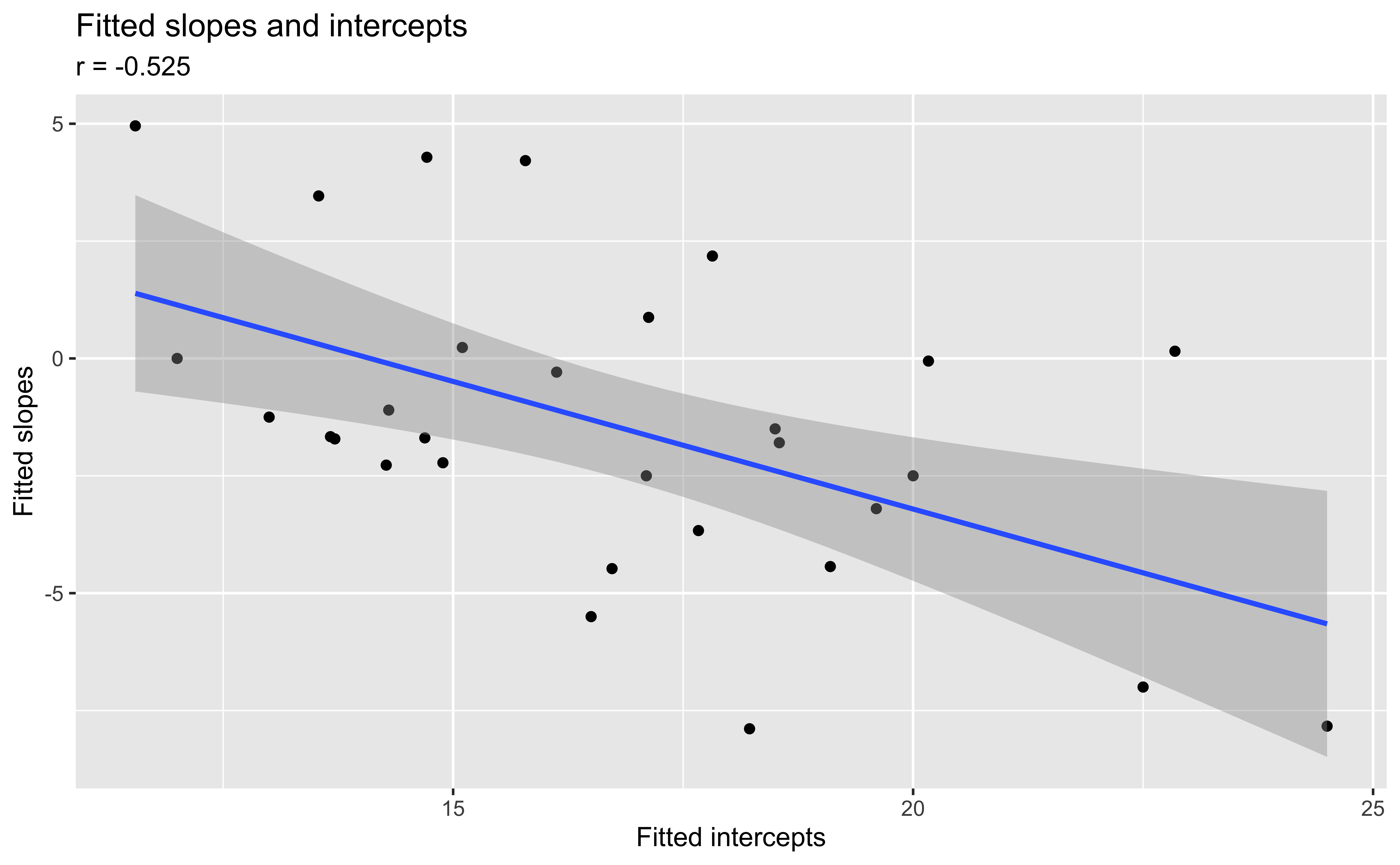
Recreated from Figure 8.11

Describe what we learn about the association between the slopes and intercepts based on this plot.

Distribution of Level Two errors

Use a multivariate normal distribution for the Level Two error terms [uivi]∼N([00],[σ2uρuvσuσvρuvσuσvσ2v])

where σ2u and σ2v are the variance of ui’s and vi’s respectively, and σuv=ρuvσuσv is covariance between ui and vi

  • What does it mean for ρuv>0?
  • What does it mean for ρuv<0?

Visualizing multivariate normal distribution

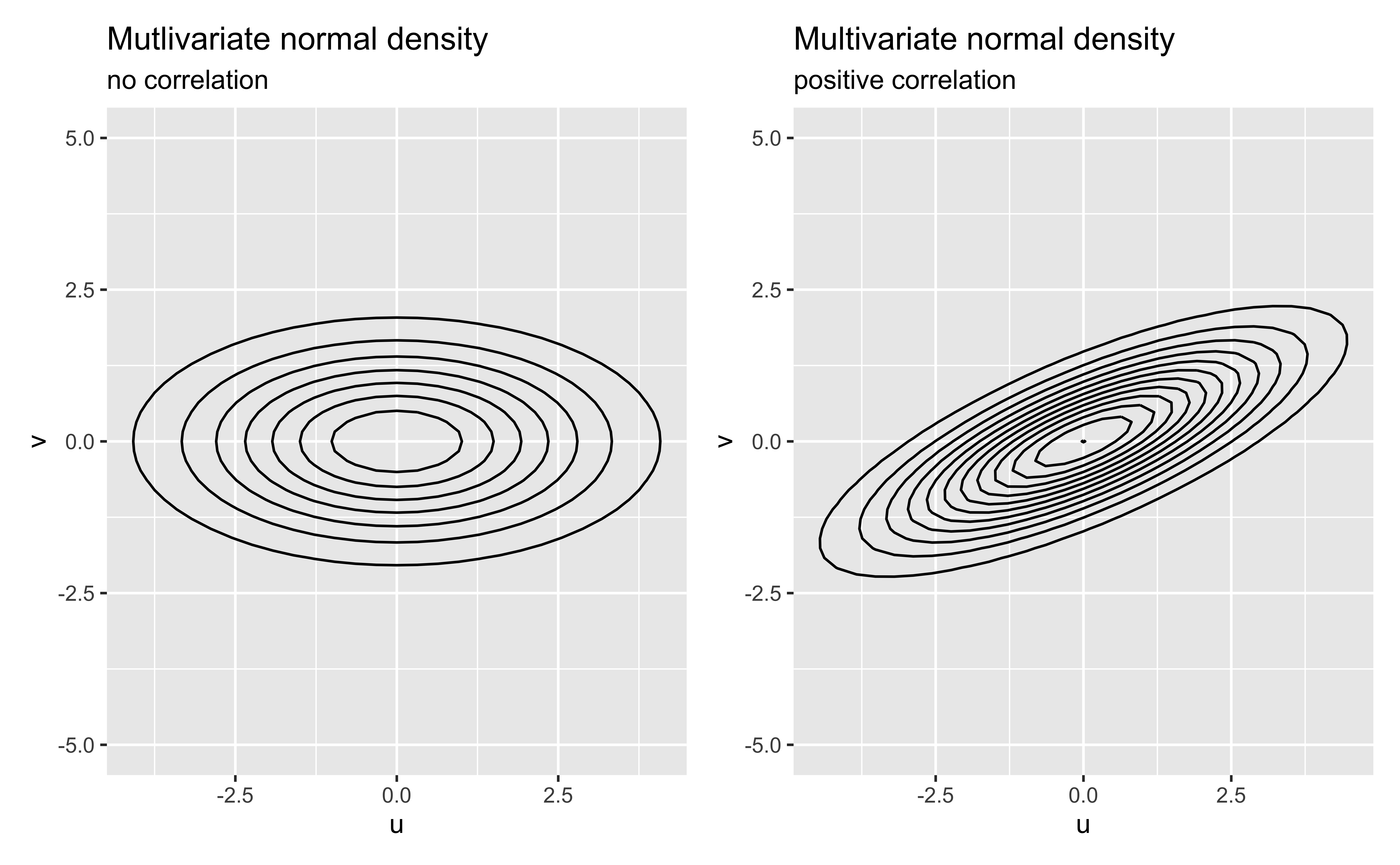
Recreated from Figure 8.12

Fit the model in R

Fit multilevel model using tidymodels and the multilevelmod R packages. Display results using the tidy() function from the broom.mixed package.

library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)library(tidymodels)
library(multilevelmod)
library(broom.mixed)

music_fit <- 
  linear_reg() |>
  set_engine("lmer") |>
  fit(na ~ orchestra + large_ensemble +
        orchestra:large_ensemble + (large_ensemble|id),
      data = music)

tidy(music_fit) |> kable(digits = 3)

Fit the model in R

effect group term estimate std.error statistic
fixed NA (Intercept) 15.930 0.641 24.833
fixed NA orchestra1 1.693 0.945 1.791
fixed NA large_ensemble1 -0.911 0.845 -1.077
fixed NA orchestra1:large_ensemble1 -1.424 1.099 -1.295
ran_pars id sd__(Intercept) 2.378 NA NA
ran_pars id cor__(Intercept).large_ensemble1 -0.635 NA NA
ran_pars id sd__large_ensemble1 0.672 NA NA
ran_pars Residual sd__Observation 4.670 NA NA

Final model

^nai=15.930+1.693 Orchestrai−0.911 LargeEnsembleij−1.424 Orchestrai:LargeEnsembleijˆσu=2.378ˆσv=0.672ˆσϵ=4.670ˆρuv=−0.635

Acknowledgements

The content in the slides is from - BMLR: Chapter 7 - Correlated data - BMLR: Chapter 8 - Introduction to Multilevel Models

  • Sadler, Michael E., and Christopher J. Miller. 2010. “Performance Anxiety: A Longitudinal Study of the Roles of Personality and Experience in Musicians.” Social Psychological and Personality Science 1 (3): 280–87. http://dx.doi.org/10.1177/1948550610370492.

🔗 Week 14

1 / 36
Fitting multilevel models Prof. Maria Tackett Nov 30, 2022

  1. Slides

  2. Tools

  3. Close
  • Fitting multilevel models
  • Announcements
  • Learning goals
  • Data: Music performance anxiety
  • Data: Music performance anxiety
  • Look at data
  • Unviariate EDA
  • Bivariate EDA
  • Bivariate EDA
  • Fitting the model
  • Questions we want to answer
  • Modeling workflow
  • 1️⃣ Level One model
  • Level One model for one student
  • Level One model for musician 22
  • Application exercise
  • Level One model summaries
  • Level Two Model
  • Application exercise
  • Estimated coefficients by instrument
  • Level Two model
  • Writing out the models
  • Composite model
  • Disadvantages to this approach
  • Application exercise
  • Unified approach to two-level modeling
  • Framework
  • Composite model
  • Error terms
  • Slopes vs intercepts by musician
  • Distribution of Level Two errors
  • Visualizing multivariate normal distribution
  • Fit the model in R
  • Fit the model in R
  • Final model
  • Acknowledgements
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help