AE 15: Introduction to Multilevel Models

Important

Go to the course GitHub organization and locate your ae-15- to get started.

The AE is due on GitHub by Thursday, December 01, 11:59pm.

Important

The AE is due on GitHub by Thursday, December 01, 11:59pm.

library(tidyverse)
library(tidymodels)
library(knitr)
library(patchwork)

music <- read_csv("data/musicdata.csv") |>
  mutate(orchestra = if_else(instrument == "orchestral instrument", 1, 0), 
         large_ensemble = if_else(perform_type == "Large Ensemble", 1, 0))

Part 1: Univariate EDA

1. Plot the distribution of the response variable negative affect (na) using individual observations.

ggplot(data  = music, aes(x = na)) + 
  geom_histogram(fill = "steelblue", color = "black", binwidth = 2) + 
  labs(x = "Individual scores", 
       title ="Distribution of Negative Affect Score")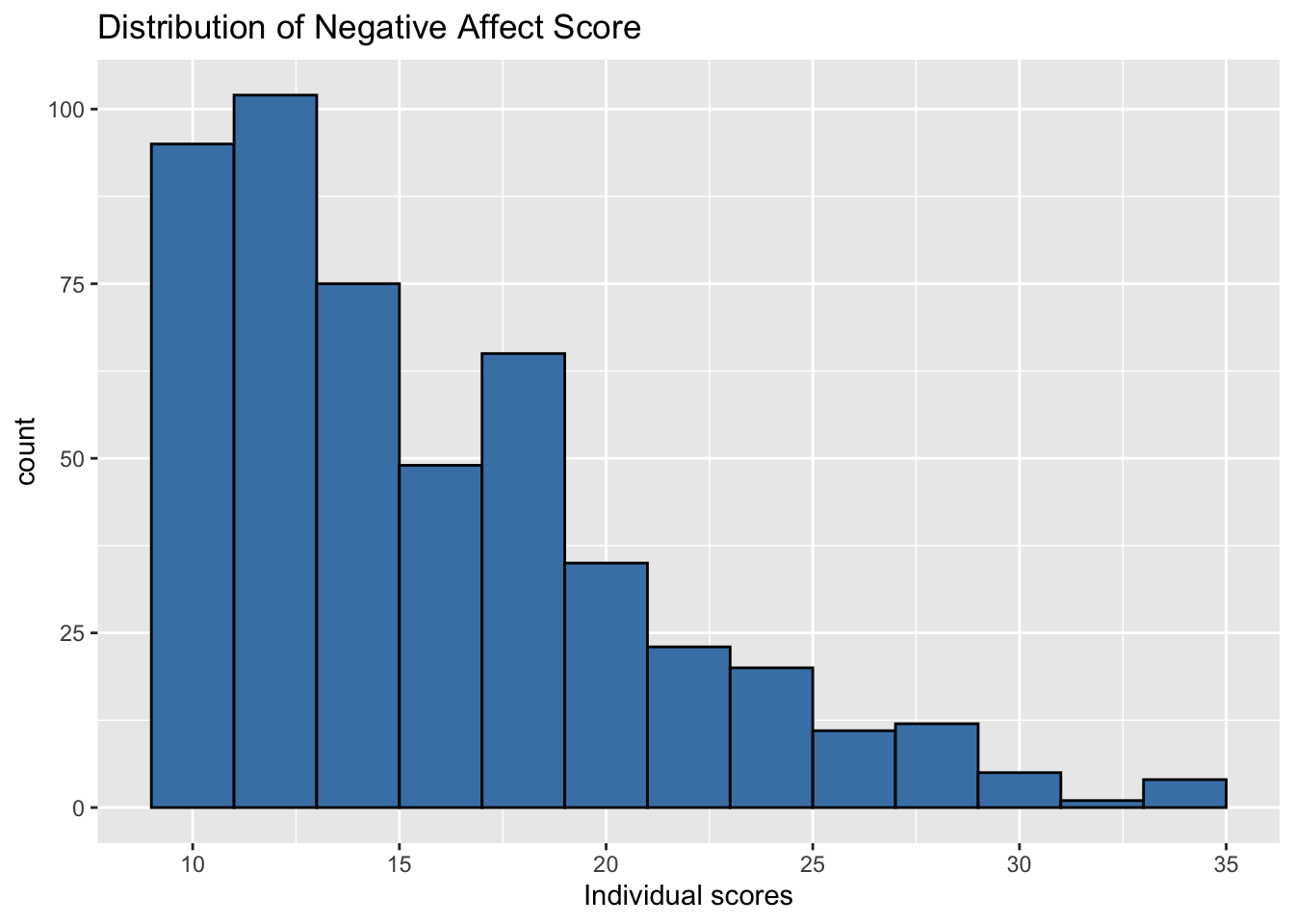

2. Plot the distribution of the response variable using an aggregated value (or single observation) for each Level Two observation (musician).

music |>
  group_by(id) |>
  summarise(mean_na = mean(na)) |>
  ungroup() |>
  ggplot(aes(x = mean_na)) + 
  geom_histogram(fill = "steelblue", color = "black", binwidth = 2) + 
  labs(x = "Mean scores", 
       title = "Distribution of Mean Negative Affect Scores",
       subtitle = "By Musician")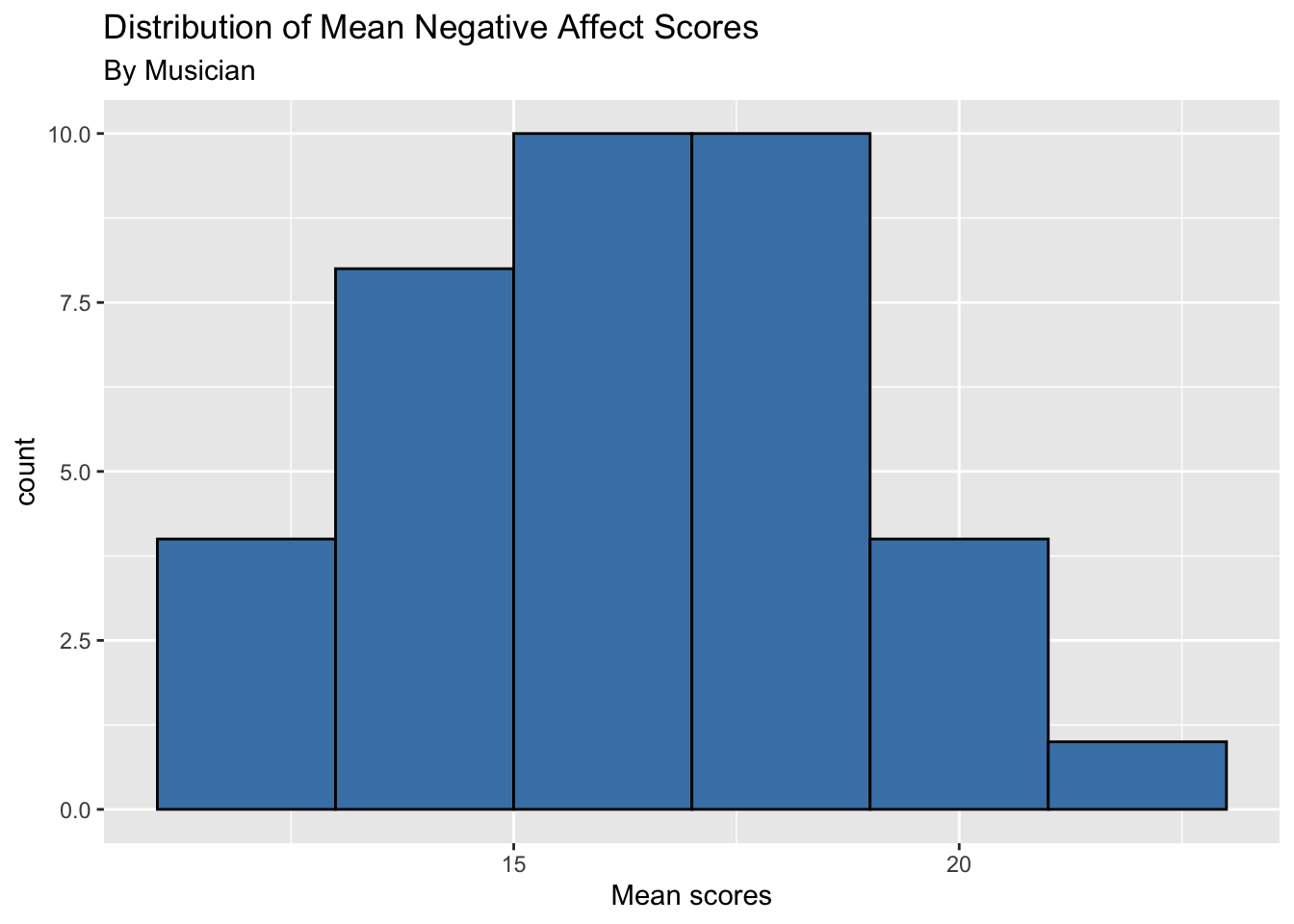

3. How do the plots compare? How do they differ?

4. What are some advantages of each plot? What are some disadvantages?

Part 2: Bivariate EDA

1. Make a single scatterplot of the negative affect versus number of previous performances (previous) using the individual observations. Use geom_smooth() to add a linear regression line to the plot.

# Add code

2. Make a separate scatterplot of the negative affect versus number of previous performances (previous) faceted by musician (id). Use geom_smooth() to add a linear regression line to each plot.

# Add code

3. How do the plots compare? How do they differ?

4. What are some advantages of each plot? What are some disadvantages?

Part 3: Level One Models

Code to fit and display the Level One model for Observation 22 is below.

id_22 <- music |>
  filter(id == 22)

linear_reg() |>
  set_engine("lm") |>
  fit(na ~ large_ensemble, data = id_22) |>
  tidy() |> kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	24.500	1.96	12.503	0.000
large_ensemble	-7.833	2.53	-3.097	0.009

Code to fit the Level One model and get the fitted slope, intercept, and \(R^2\) values for all musicians is below.

# set up tibble for fitted values 

model_stats <- tibble(slopes = rep(0,37), 
               intercepts = rep(0,37), 
               r.squared = rep(0, 37))


ids <- music |> distinct(id) |> pull()

# counter to keep track of row number to store model_stats

count <- 1

for(i in ids){
  
id_data <- music |>
  filter(id == i)

level_one_model <- linear_reg() |>
  set_engine("lm") |>
  fit(na ~ large_ensemble, data = id_data) 

level_one_model_tidy <- tidy(level_one_model)

model_stats$slopes[count] <- level_one_model_tidy$estimate[2]
model_stats$intercepts[count] <- level_one_model_tidy$estimate[1]
model_stats$r.squared[count] <- glance(level_one_model)$r.squared

count = count + 1
}

Part 4: Level Two Models

# Make a Level Two data set
musicians <- music |>
  distinct(id, orchestra) |>
  bind_cols(model_stats)

Model for intercepts

a <- linear_reg() |>
  set_engine("lm") |>
  fit(intercepts ~ orchestra, data = musicians) 

tidy(a) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	16.283	0.671	24.249	0.000
orchestra	1.411	0.991	1.424	0.163

Model for slopes

b <- linear_reg() |>
  set_engine("lm") |>
  fit(slopes ~ orchestra, data = musicians) 

tidy(b) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	-0.771	0.851	-0.906	0.373
orchestra	-1.406	1.203	-1.168	0.253

Part 5: Distribution of \(R^2\) values

ggplot(data = model_stats, aes(x = r.squared)) +
  geom_dotplot(fill = "steelblue",  color = "black") +
  labs(x = "R-squared values", 
       title = "Distribution of R-squared of Level One models")