AE 08: Feature Engineering- Model workflow

The Office

Published

October 5, 2022

Important

Go to the course GitHub organization and locate your ae-08- to get started.

The AE is due on GitHub by Saturday, October 08 at 11:59pm.

Packages

library(tidyverse)
library(tidymodels)
library(viridis)
library(knitr)

Load data

office_ratings <- read_csv("data/office_ratings.csv")

Exploratory data analysis

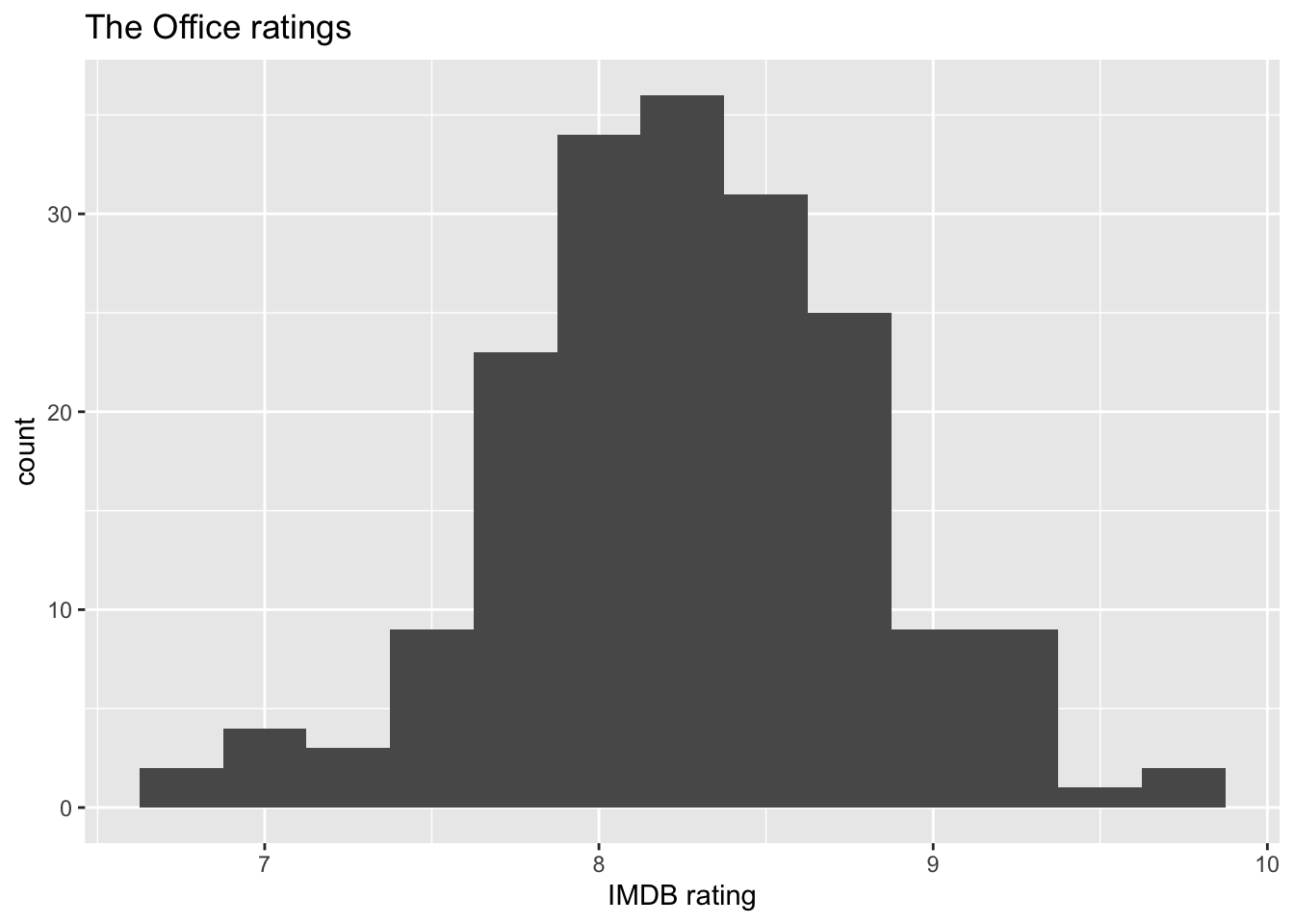
Below are two of the exploratory data analysis plots from lecture.

ggplot(office_ratings, aes(x = imdb_rating)) +
  geom_histogram(binwidth = 0.25) +
  labs(
    title = "The Office ratings",
    x = "IMDB rating"
  )

office_ratings |>
  mutate(season = as_factor(season)) |>
  ggplot(aes(x = season, y = imdb_rating, color = season)) +
  geom_boxplot() +
  geom_jitter() +
  guides(color = "none") +
  labs(
    title = "The Office ratings",
    x = "Season",
    y = "IMDB rating"
  ) +
  scale_color_viridis_d()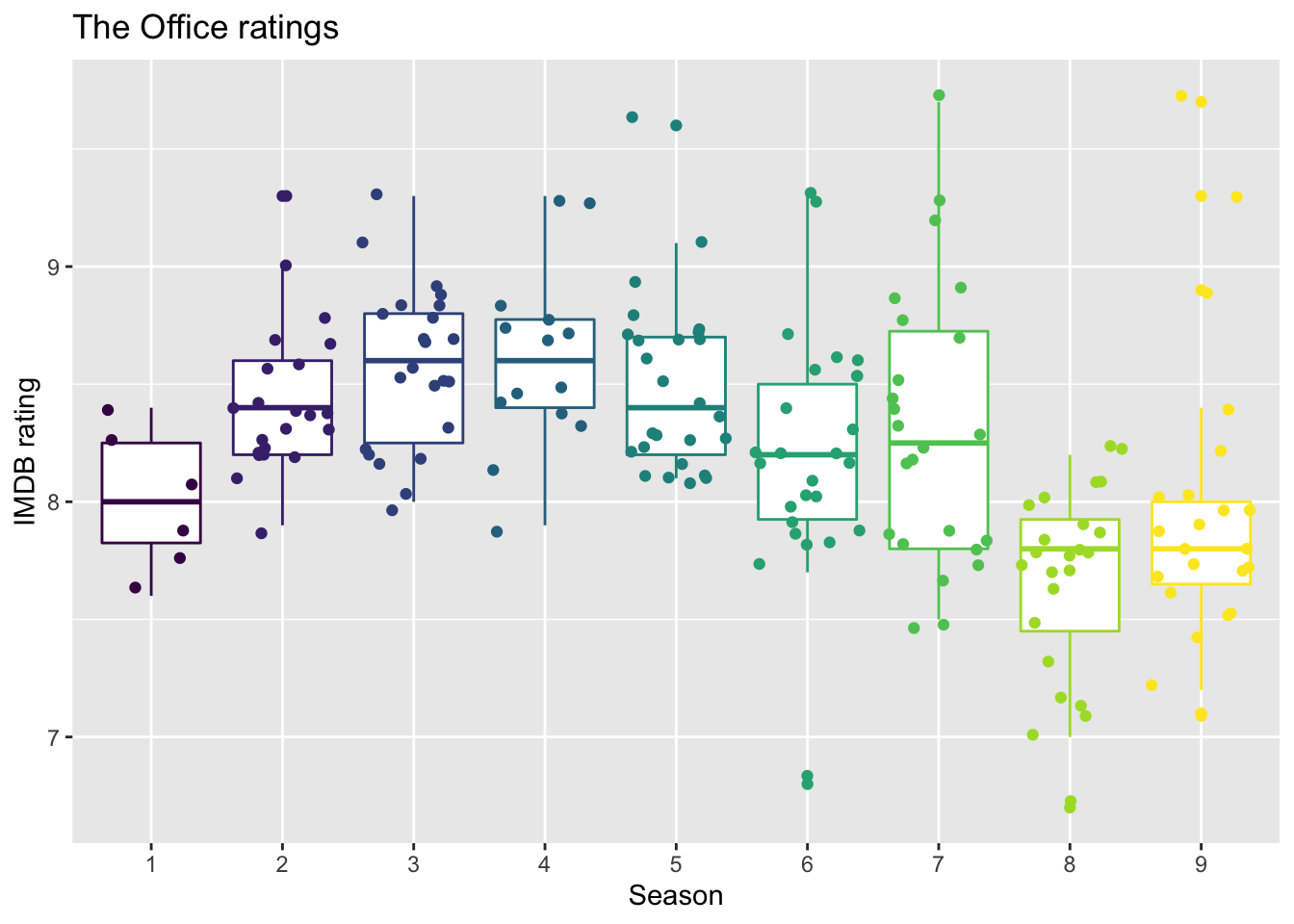

Test/train split

set.seed(123)
office_split <- initial_split(office_ratings) # prop = 3/4 by default
office_train <- training(office_split)
office_test  <- testing(office_split)

Build a recipe

office_rec <- recipe(imdb_rating ~ ., data = office_train) |>
  # make title's role ID
  update_role(title, new_role = "ID") |>
  # extract day of week and month of air_date
  step_date(air_date, features = c("dow", "month")) |>
  # identify holidays and add indicators
  step_holiday(
    air_date, 
    holidays = c("USThanksgivingDay", "USChristmasDay", "USNewYearsDay", "USIndependenceDay"), 
    keep_original_cols = FALSE
  ) |>
  # turn season into factor
  step_num2factor(season, levels = as.character(1:9)) |>
  # make dummy variables
  step_dummy(all_nominal_predictors()) |>
  # remove zero variance predictors
  step_zv(all_predictors())
office_rec
Recipe

Inputs:

      role #variables
        ID          1
   outcome          1
 predictor          4

Operations:

Date features from air_date
Holiday features from air_date
Factor variables from season
Dummy variables from all_nominal_predictors()
Zero variance filter on all_predictors()

Workflows and model fitting

Specify model

office_spec <- linear_reg() |>
  set_engine("lm")

office_spec
Linear Regression Model Specification (regression)

Computational engine: lm

Build workflow

office_wflow <- workflow() |>
  add_model(office_spec) |>
  add_recipe(office_rec)
office_wflow
══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: linear_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
5 Recipe Steps

• step_date()
• step_holiday()
• step_num2factor()
• step_dummy()
• step_zv()

── Model ───────────────────────────────────────────────────────────────────────
Linear Regression Model Specification (regression)

Computational engine: lm

Fit model to training data

office_fit <- office_wflow |>
  fit(data = office_train)

tidy(office_fit) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 6.396 0.510 12.532 0.000
episode -0.004 0.017 -0.230 0.818
total_votes 0.000 0.000 9.074 0.000
season_X2 0.811 0.327 2.482 0.014
season_X3 1.042 0.343 3.040 0.003
season_X4 1.090 0.295 3.695 0.000
season_X5 1.082 0.348 3.109 0.002
season_X6 1.004 0.367 2.735 0.007
season_X7 1.018 0.352 2.894 0.005
season_X8 0.497 0.348 1.430 0.155
season_X9 0.621 0.345 1.802 0.074
air_date_dow_Tue 0.382 0.422 0.904 0.368
air_date_dow_Thu 0.284 0.389 0.731 0.466
air_date_month_Feb -0.060 0.132 -0.452 0.652
air_date_month_Mar -0.075 0.156 -0.481 0.631
air_date_month_Apr 0.095 0.177 0.539 0.591
air_date_month_May 0.156 0.213 0.734 0.464
air_date_month_Sep -0.078 0.223 -0.348 0.728
air_date_month_Oct -0.176 0.174 -1.014 0.313
air_date_month_Nov -0.156 0.149 -1.046 0.298
air_date_month_Dec 0.170 0.149 1.143 0.255

Evaluate model on training data

Make predictions

Important

Fill in the code and make #| eval: true before rendering the document.

office_train_pred <- predict(office_fit, ______) |>
  bind_cols(_____)

Calculate R2

Important

Fill in the code and make #| eval: true before rendering the document.

rsq(office_train_pred, truth = _____, estimate = _____)
  • What is preferred - high or low values of R2?

Calculate RMSE

Important

Fill in the code and make #| eval: true before rendering the document.

rmse(______, ________, ________)

  • What is preferred - high or low values of RMSE?

  • Is this RMSE considered high or low? Hint: Consider the range of the response variable to answer this question.

    office_train |>
  summarise(min = min(imdb_rating), max = max(imdb_rating))
    # A tibble: 1 × 2
    min   max
  <dbl> <dbl>
1   6.7   9.7

Evaluate model on testing data

Answer the following before evaluating the model performance on testing data:

  • Do you expect R2 on the testing data to be higher or lower than the R2 calculated using training data? Why?

  • Do you expect RMSE on the testing data to be higher or lower than the R2 calculated using training data? Why?

Make predictions

# fill in code to make predictions from testing data

Calculate R2

# fill in code to calculate $R^2$ for testing data

Calculate RMSE

# fill in code to calculate RMSE for testing data

Compare training and testing data results

  • Compare the R2 for the training and testing data. Is this what you expected?

  • Compare the RMSE for the training and testing data. Is this what you expected?