AE 09: Model comparison

Restaurant tips

Published

October 19, 2022

Important

Go to the course GitHub organization and locate your ae-09- to get started.

The AE is due on GitHub by Saturday, October 22 at 11:59pm.

Packages

library(tidyverse)
library(tidymodels)
library(viridis)
library(knitr)
library(patchwork)

Load data

tips <- read_csv("data/tip-data.csv") |>
  filter(!is.na(Party))
# relevel factors
tips <- tips |>
  mutate(
    Meal = fct_relevel(Meal, "Lunch", "Dinner", "Late Night"),
    Age  = fct_relevel(Age, "Yadult", "Middle", "SenCit")
  )

Exploratory data analysis

Response variable

ggplot(tips, aes(x = Tip)) +
  geom_histogram(binwidth = 1) +
  labs(title = "Distribution of tips")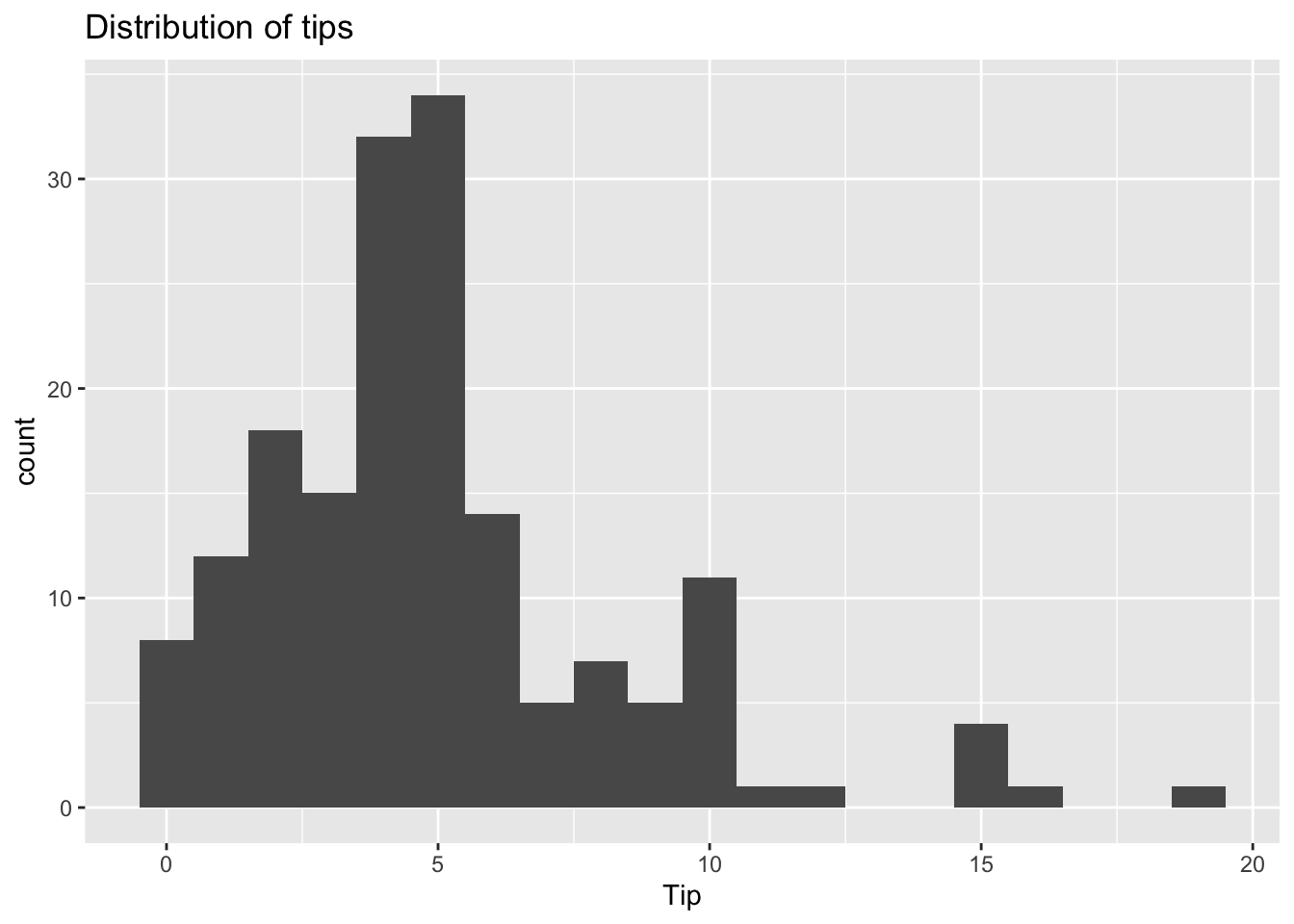

Predictor variables

p1 <- ggplot(tips, aes(x = Party)) +
  geom_histogram(binwidth = 1) +
  labs(title = "Number of people in party")

p2 <- ggplot(tips, aes(x = Meal, fill = Meal)) +
  geom_bar() +
  labs(title = "Meal type") +
  scale_fill_viridis_d()

p3 <- ggplot(tips, aes(x = Age, fill = Age)) +
  geom_bar() +
  labs(title = "Age of payer") +
  scale_fill_viridis_d(option = "E", end = 0.8)

p1 + (p2 / p3)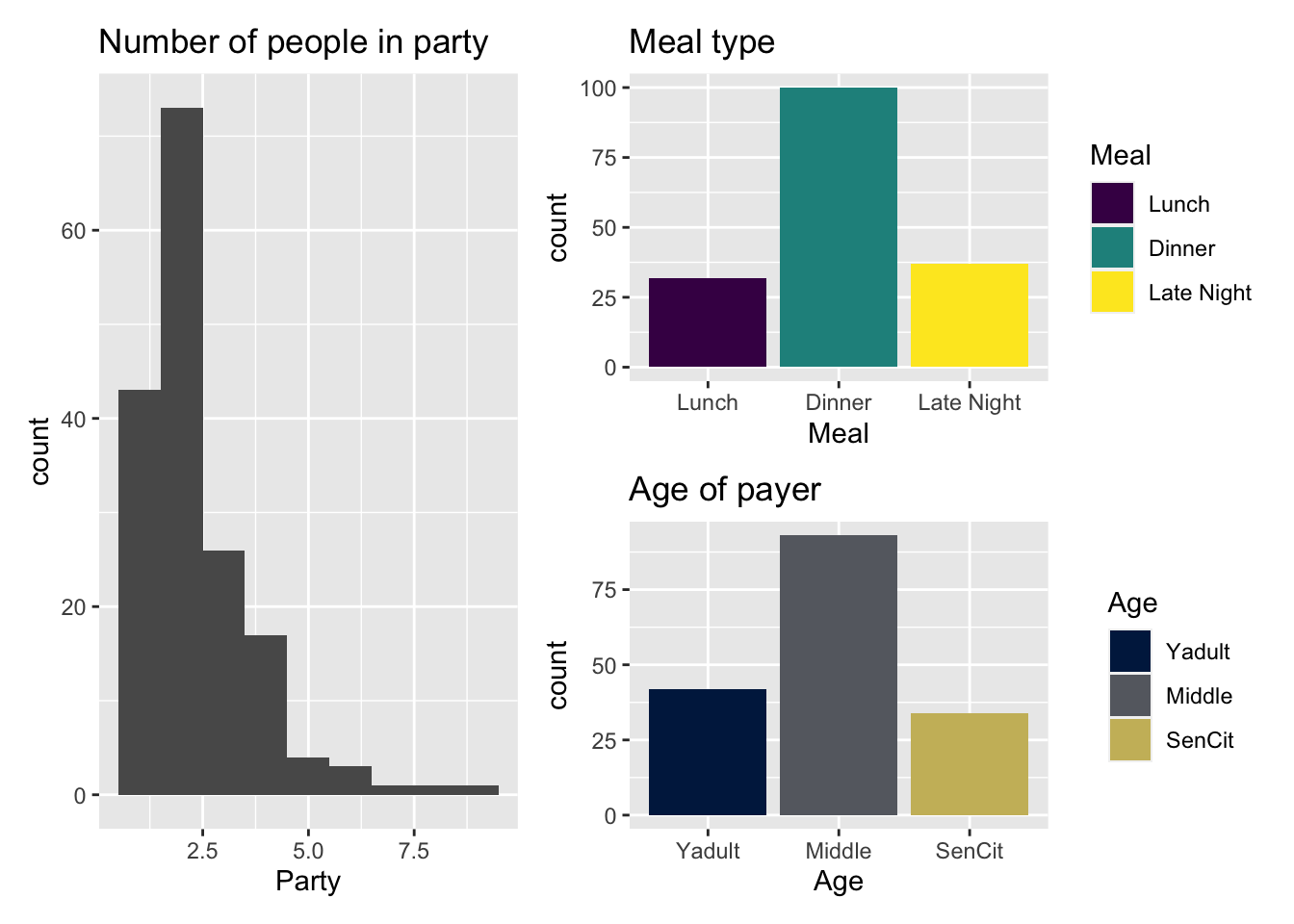

Response vs. predictors

p4 <- ggplot(tips, aes(x = Party, y = Tip)) +
  geom_point(color = "#5B888C")

p5 <- ggplot(tips, aes(x = Meal, y = Tip, fill = Meal)) +
  geom_boxplot(show.legend = FALSE) +
  scale_fill_viridis_d()

p6 <- ggplot(tips, aes(x = Age, y = Tip, fill = Age)) +
  geom_boxplot(show.legend = FALSE) +
  scale_fill_viridis_d(option = "E", end = 0.8)

p4 + p5 + p6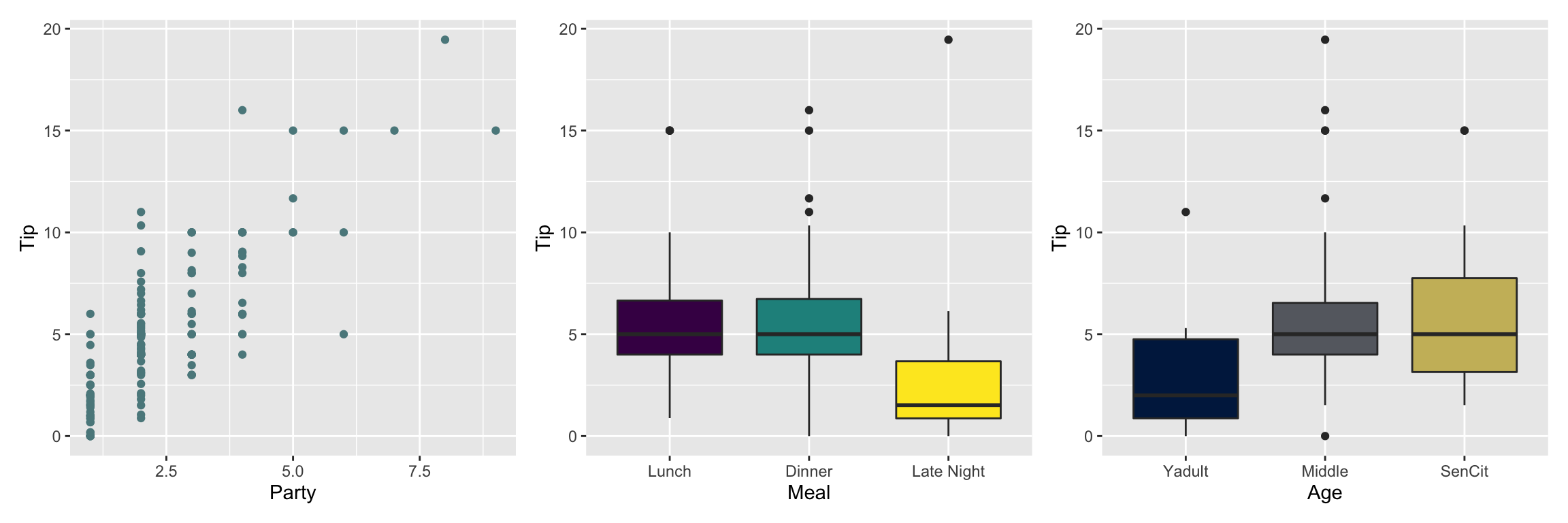

Models

Model 1: Tips vs. Age & Party

tip_fit <- linear_reg() |>
  set_engine("lm") |>
  fit(Tip ~ Party + Age, data = tips)

tidy(tip_fit) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) -0.170 0.366 -0.465 0.643
Party 1.837 0.124 14.758 0.000
AgeMiddle 1.009 0.408 2.475 0.014
AgeSenCit 1.388 0.485 2.862 0.005

Model 2: Tips vs. Age, Party, Meal & Day

tip_fit_2 <- linear_reg() |>
  set_engine("lm") |>
  fit(Tip ~ Party +  Age + Meal +  Day, 
      data = tips)

tidy(tip_fit_2) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) -0.354 0.968 -0.365 0.715
Party 1.792 0.126 14.179 0.000
AgeMiddle 0.506 0.427 1.185 0.238
AgeSenCit 1.017 0.494 2.058 0.041
MealDinner 0.636 0.457 1.390 0.167
MealLate Night -0.729 0.754 -0.967 0.335
DaySaturday 0.812 0.783 1.038 0.301
DaySunday 0.097 0.877 0.111 0.912
DayThursday 0.069 0.897 0.077 0.939
DayTuesday 0.414 0.670 0.618 0.537
DayWednesday 0.936 1.098 0.853 0.395

Why did we not use the full recipe() workflow to fit Model 1 or Model 2?

\(R^2\) and Adjusted \(R^2\)

Fill in the code below to calculate \(R^2\) and Adjusted \(R^2\) for Model 1. Put eval: true once the code is updated.

glance(______) |>
  select(r.squared, adj.r.squared)

Calculate \(R^2\) and Adjusted \(R^2\) for Model 2.

# r-sq and adj. r-sq for model 2

We would like to choose the model that better fits the data.

  • Which model would we choose based on \(R^2\)?

  • Which model would we choose based on Adjusted \(R^2\)?

  • Which statistic should we use to choose the final model - \(R^2\) or Adjusted \(R^2\)? Why?

AIC & BIC

Use the glance() function to calculate AIC and BIC for Models 1 and 2.

## AIC and BIC for Model 1
## AIC and BIC for Model 2

We would like to choose the model that better fits the data.

  • Which model would we choose based on AIC?

  • Which model would we choose based on BIC?

Evaluating analysis process

We fit and evaluated these models using the entire data set. What is a limitation to using the entire data set to fit and evaluate models?